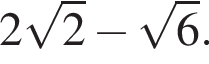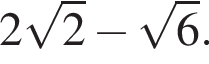В пирамиде SАВС угол АSВ равен 60°, а углы ВSС и СSА — по 45°.
а) Докажите, что плоскости ВSС и АSС перпендикулярны.
б) Найдите радиус сферы вписанной в пирамиду SABC, если известно, что 
Решение. а) По теореме косинусов для трехгранного угла имеем:
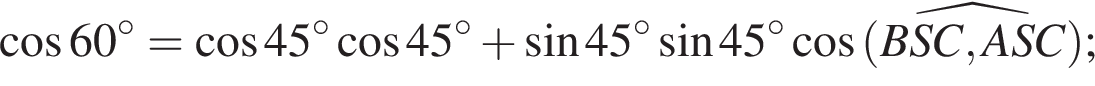
Значит, плоскости перпендикулярны.
б) Треугольник 
равнобедренный с углом, противолежащим основанию, 
поэтому он — равносторонний, 
Треугольники 
и 
равны равнобедренному прямоугольному треугольнику с катетом 
по первому признаку, поэтому 
Значит, площадь поверхности пирамиды равна:
Теперь вычислим ее объем. По теореме о трех перпендикулярах проекцией S на 
должна быть такая точка 
что прямая TB перпендикулярна прямой CB и прямая TA перпендикулярна прямой CA. Тогда 
— треугольник с углами 
и 
поэтому:
Тогда:
Теперь найдём объём пирамиды SABC:
Радиус вписанной сферы равен:
Ответ: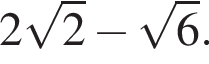 
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Обоснованно получен верный ответ. | 2 |
| Решение содержит обоснованный переход к планиметрической задаче, но получен неверный ответ или решение не закончено ИЛИ при правильном ответе решение недостаточно обосновано. | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше. | 0 |