Тип 18 № 516765 
Источники:
Классификатор алгебры: Уравнения с параметром, Уравнения смешанного типа
Методы алгебры: Перебор случаев, Перебор случаев
Задача с параметром. Аналитическое решение уравнений и неравенств
i
Найдите все такие значения параметра a, при каждом из которых уравнение 
имеет решения на отрезке 
Решение. Заметим, что
Преобразуем уравнение:
Рассмотрим два случая.
Пусть 
тогда из неравенства
отрезку 
принадлежат два числа 
и 
Пусть 
тогда имеем:
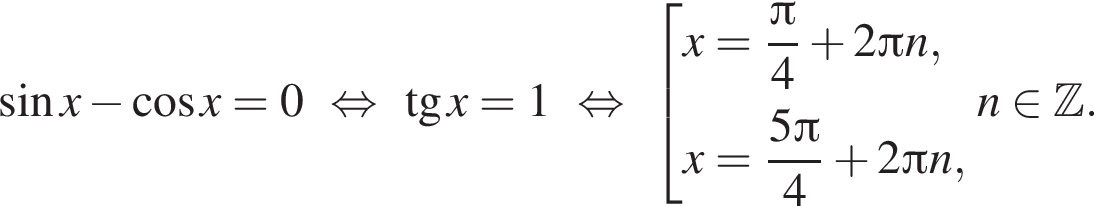
В первой серии не содержится корней, лежащих на отрезке Среди корней, содержащихся во второй серии, отрезку принадлежит одно число 
Подставляя его в неравенство, получаем: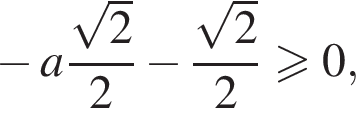 
откуда 
Ответ: 
Критерии проверки:
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Обоснованно получен правильный ответ. | 4 |
| С помощью верного рассуждения получено множество значений a, отличающееся от искомого конечным числом точек. | 3 |
| С помощью верного рассуждения получены все граничные точки искомого множества значений a. | 2 |
| Верно найдена хотя бы одна граничная точка искомого множества значений a. | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше. | 0 |
Ответ:
516765
Классификатор алгебры: Уравнения с параметром, Уравнения смешанного типа
Методы алгебры: Перебор случаев, Перебор случаев