Найдите все значения а, при каждом из которых система уравнений
имеет ровно четыре различных решения.
Решение. Сделаем замену 
и заметим, что 
Очевидно, число решений системы будет совпадать с числом решений уравнения 
Очевидно, 
является его решением при всех a.
При 
уравнение сводится к 
Это уравнение имеет два положительных корня, если 
то есть при 
и один положительный корень при 
или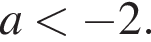 
При 
уравнение сводится к 
Это уравнение имеет два отрицательных корня, если 
то есть при 
и один отрицательный корень при 
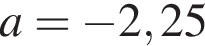или 
Поэтому нужное количество корней будет при 
Ответ: 
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Обоснованно получен правильный ответ. | 4 |
| C помощью верного рассуждения получено множество значений a, отличащееся от искомого только включением/исключением точки а = −3 | 3 |
C помощью верного рассуждения получен один из промежутков множества значений a:  или  ; возможно, с включением граничных точек | 2 |
| Задача верно сведена к исследованию взаимного расположения дуг окружностей и прямых (аналитически и графически) ИЛИ получен неверный ответ из-за вычислительной ошибки, но при этом верно выполнены все шаги решения | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше. | 0 |
| Максимальный балл: | 4 |