i
В выпуклом четырёхугольнике ABCD точки K, M, P, E — середины сторон AB, BC, CD, и DA соответственно.
а) Докажите, что площадь четырёхугольника KMPE равна половине площади четырёхугольника ABCD.
б) Найдите большую диагональ четырёхугольника KMPE, если известно, что AC = 6, BD = 8, а сумма площадей треугольников AKE и CMP равна 
Аналогично 
поэтому треугольники AKE и MCP имеют суммарную площадь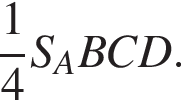 
Аналогично и треугольники BKM и EPD. Значит, на долю KMPE приходится 
что и требовалось.
и 
поэтому KMPE — параллелограмм. Причем 
откуда углы параллелограмма — 60° и 120°. В таком случае его большая диагональ равна по теореме косинусов 
