i
Даны треугольники ABC и A1B1C1. Прямые AA1, BB1, CC1 пересекаются в одной точке. Прямые AB и A1B1 пересекаются в точке C2. Прямые АС и A1C1 пересекаются в точке B2. Прямые BC и B1C1 пересекаются в точке A2.
а) Докажите, что точки A2, B2, C2 лежат на одной прямой.
б) Найдите отношение площади треугольника A1B1C1 и площади треугольника ABC, если высоты треугольника ABC равны  а высоты треугольника A1B1C1 равны
а высоты треугольника A1B1C1 равны 


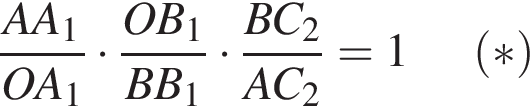

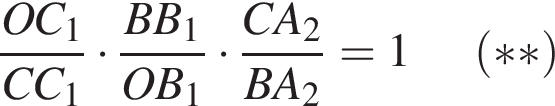
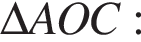


 что удовлетворяет условию теоремы Менелая относительно принадлежности точек:
что удовлетворяет условию теоремы Менелая относительно принадлежности точек:  одной прямой.
одной прямой. — стороны
— стороны  При этом
При этом  — соответствующие его высоты. Тогда:
— соответствующие его высоты. Тогда: 









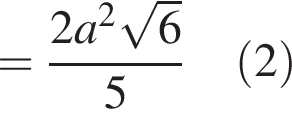
 — стороны
— стороны  При этом
При этом  — соответствующие его высоты. Тогда:
— соответствующие его высоты. Тогда: 




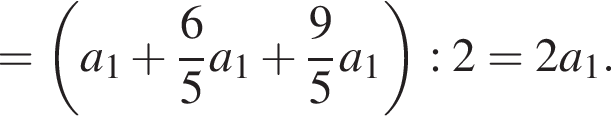



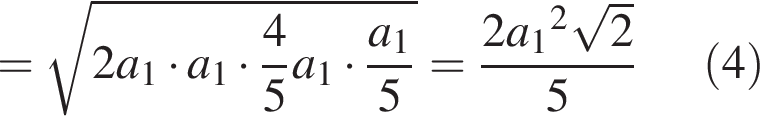









 Следовательно, мы вправе равенство (5) переписать так:
Следовательно, мы вправе равенство (5) переписать так: 
 получим:
получим: 
