i
А) Представьте 1 в виде суммы трех попарно различных дробей вида 
где n — натуральное число.
Б) Представьте 1 в виде суммы пяти попарно различных дробей вида где n — натуральное число.
В) Докажите, что 1 можно представить в виде суммы любого (большего двух) количества попарно различных дробей вида где n — натуральное число.
Получим: 
Значит, 
Пусть мы представили единицу в виде суммы k дробей с числителем 1. Возьмем меньшую из этих дробей и представим ее в следующем виде: 
Таким образом, получим представление единицы в виде суммы k+2 дробей нужного вида. Значит, из суммы четырех дробей можно получить сумму 6,8,10, ... дробей, а из суммы 5 дробей можно получить сумму 7,9,11,... дробей. Утверждение доказано.
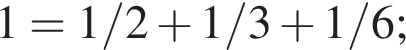б)