Найдите все корни уравнения sin(2x) = 1, удовлетворяющие неравенству 
Решение. Последовательно получаем:
Для решения неравенства 
воспользуемся геометрическим смыслом модуля. Левая ее часть на числовой прямой представляет собой сумму расстояний от точки 
до точек (1) и (8) не больше 7. Следовательно, верно неравенство
Теперь найдем целочисленные значения x, удовлетворяющие условию 
Если n = 0, то: 
Ясно, что 
Докажем, что 
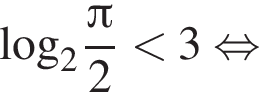
(неравенство очевидное).
Если n = 1, то 
Очевидно, что 
Докажем, что 
Действительно, 
Получили очевидное неравенство.
Заметим, что при 
будет выполнено неравенство 
Действительно, уже при 
имеем:
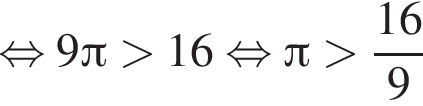
(неравенство очевидное).
Ответ: 
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Обоснованно получены верные ответы в обоих пунктах. | 2 |
| Обоснованно получен верный ответ в пункте а, или в пункте б. ИЛИ получены неверные ответы из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения обоих пунктов — пункта а и пункта б. | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше. | 0 |
| Максимальный балл | 2 |