Дано уравнение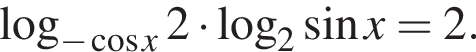 
А) Решите уравнение.
Б) Укажите корни этого уравнения, принадлежащие отрезку 
Решение. А) Найдем ограничения на x.
Отсюда ясно, что искомые решения неравенства принадлежат второй четверти.
Для таких x:
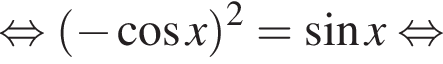
С учетом полученных ограничений на x: 
исходному уравнению удовлетворяют числа вида 
Б) Ни один корень уравнения не принадлежит отрезку Докажем это.
На единичной окружности выделен отрезок
Заметим, что и начало отрезка, точка 
и его конец, точка 
принадлежат второй четверти.
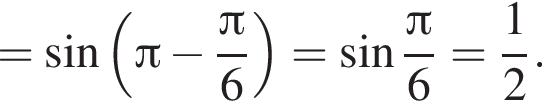
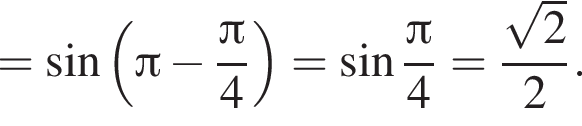
Предположим, что при некотором целочисленном значении n во второй четверти найдется число, синус которого принадлежит либо промежутку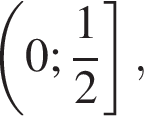 
либо промежутку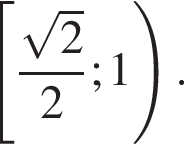 
Однако такого числа нет, так как 
Докажем это:
Ответ: А) 
Б) Таких корней нет.
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Обоснованно получены верные ответы в обоих пунктах. | 2 |
| Обоснованно получен верный ответ в пункте а, или в пункте б. ИЛИ получены неверные ответы из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения обоих пунктов — пункта а и пункта б. | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше. | 0 |
| Максимальный балл | 2 |
Б) Таких корней нет. Б) Таких корней нет.