Дано уравнение 
а) Решите уравнение.
б) Укажите корни этого уравнения, принадлежащие отрезку 
Решение. а) Рассмотрим уравнение
Заметим, что при 
При таком значении 
выражение 
теряет смысл. А при 
выражение имеет значение равное 
Заметим также, что при 
и исходное уравнение смысла не имеет.
Теперь рассмотрим уравнение 
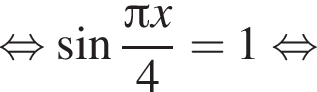
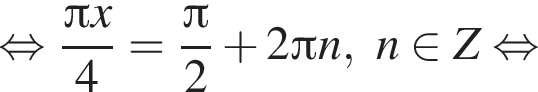
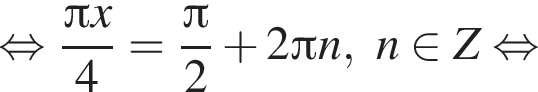
Однако при 
получим: 
при котором уравнение смысла не имеет, как это было показано выше.
Следовательно, решения заданного уравнения: 
б) Заметим, что корень уравнения, равный 3, принадлежит заданному отрезку. Для нахождения других искомых корней решим двойное неравенство 
относительно целого n при условии, что 
При 
при 
при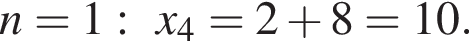 
Ответ: а) б) 
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Обоснованно получены верные ответы в обоих пунктах. | 2 |
| Обоснованно получен верный ответ в пункте а, или в пункте б. ИЛИ получены неверные ответы из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения обоих пунктов — пункта а и пункта б. | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше. | 0 |
| Максимальный балл | 2 |
б) б)