Тип Д12 C3 № 508132 
Классификатор алгебры: Неравенства с логарифмами по переменному основанию
Методы алгебры: Введение замены
Кодификатор ФИПИ/Решу ЕГЭ: 2.2.9 Метод интервалов
Сложные неравенства. Неравенства различных типов
i
Решите неравенство 
Решение. Найдем ограничения на x.
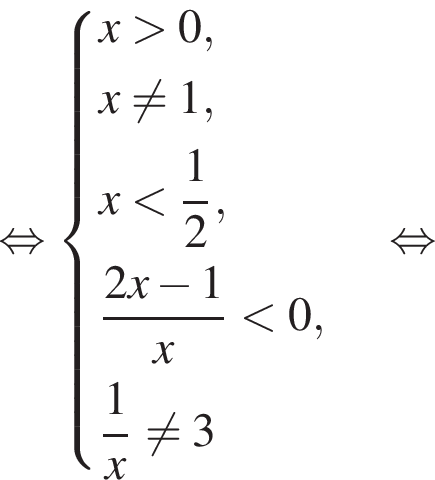
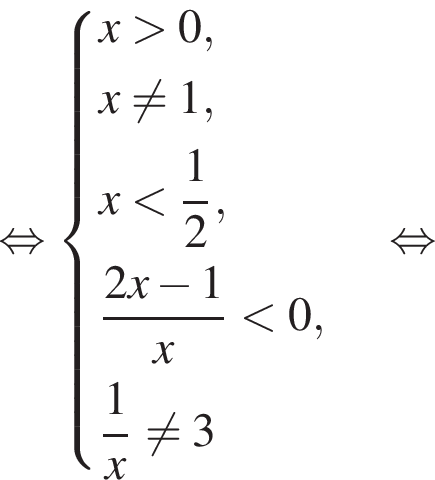
Для таких x:
Введем новую переменную. Пусть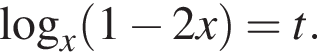 
Тогда:
При 
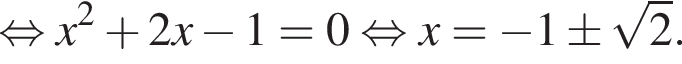
Корень последнего уравнения, равный 
не удовлетворяет ограничениям на x. Покажем, что 
Действительно, 
(неравенство очевидное).
При 
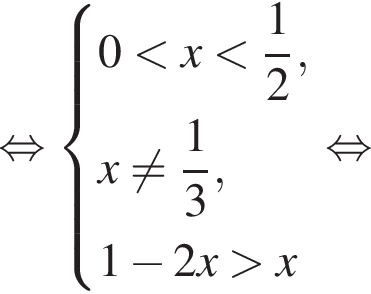
Таким образом, решения исходного неравенства — элементы множества 
Ответ:
Критерии проверки:
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Обоснованно получен верный ответ. | 3 |
| Обоснованно получены верные ответы в обоих неравенствах исходной системы. | 2 |
| Обоснованно получен верный ответ в одном неравенстве исходной системы. ИЛИ получен неверный ответ из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения системы неравенств. | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше. | 0 |
| Максимальный балл | 3 |
Ответ:
508132
Классификатор алгебры: Неравенства с логарифмами по переменному основанию
Методы алгебры: Введение замены
Кодификатор ФИПИ/Решу ЕГЭ: 2.2.9 Метод интервалов