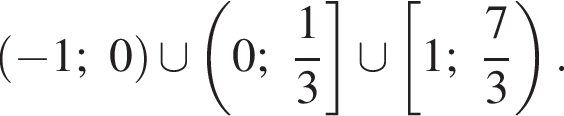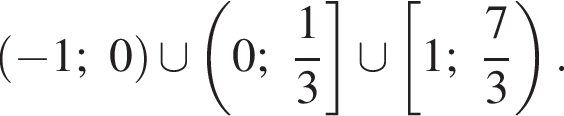Решите систему неравенств: 
Решение. Пусть 
тогда 
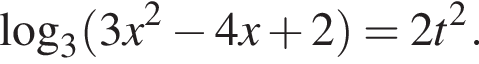Имеем:
Вернёмся к исходной переменной:
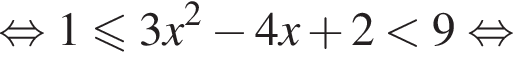
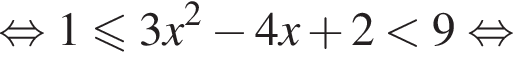
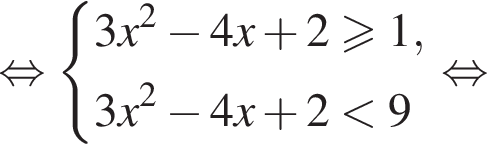
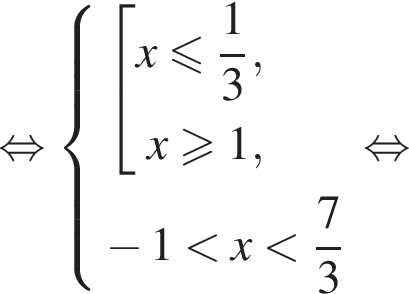
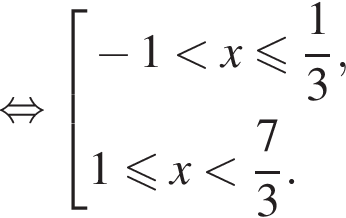
Итак, найдено множество решений второго неравенства: 
Теперь решим первое неравенство системы. Найдем ограничения на 
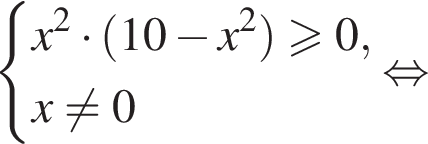
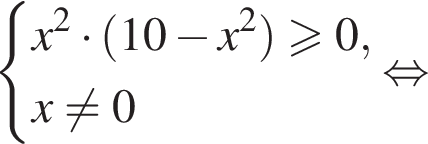
Рассмотрим первое неравенство с учетом полученных ограничений:
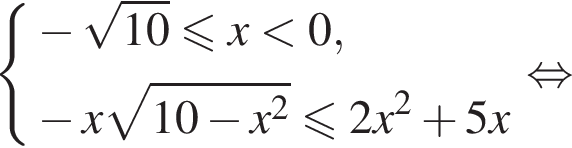
Заметим, что второе неравенство, а вместе с ним и вся полученная система выполнены, если 
то есть при 
Тогда решениями системы является интервал 
Случай 
не лежит во множестве решений первого неравенства. Далее,
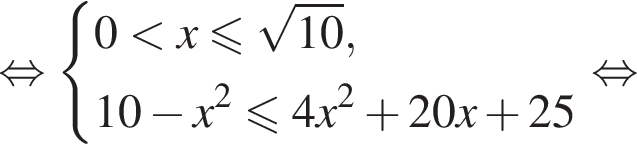
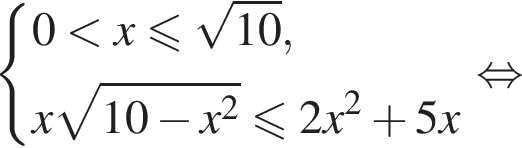
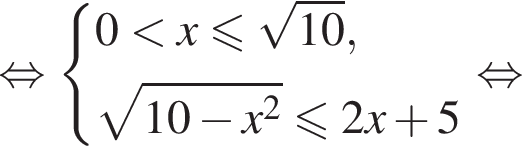
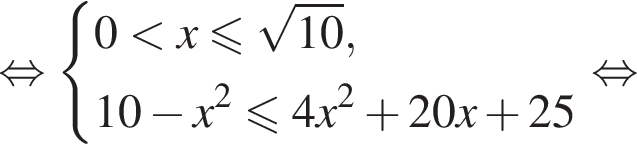
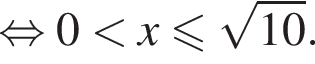
Таким образом, найдено множество решений первого неравенства системы: 
Пересечением решений обоих неравенств будет множество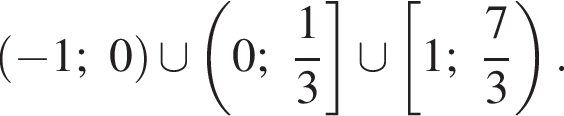 
Ответ: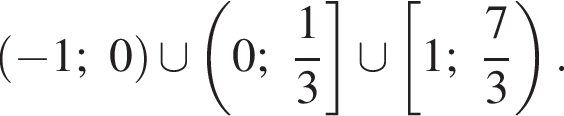
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Обоснованно получен верный ответ. | 3 |
| Обоснованно получены верные ответы в обоих неравенствах исходной системы. | 2 |
| Обоснованно получен верный ответ в одном неравенстве исходной системы. ИЛИ получен неверный ответ из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения системы неравенств. | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше. | 0 |
| Максимальный балл | 3 |