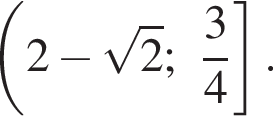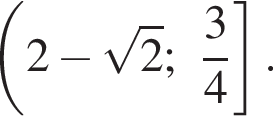Решите систему неравенств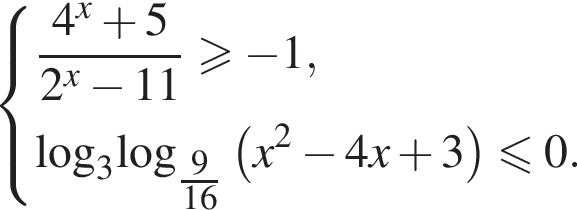 
Решение. Рассмотрим первое неравенство системы:
Решением первого неравенства системы является множество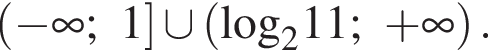 
Решим второе неравенство системы. Найдем ограничения на 
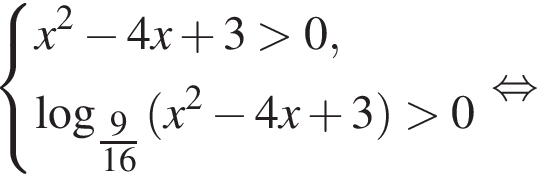
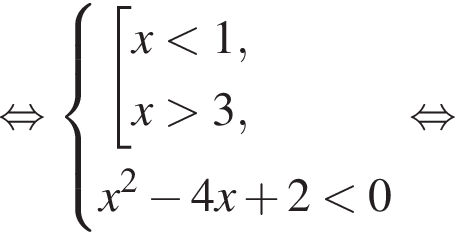
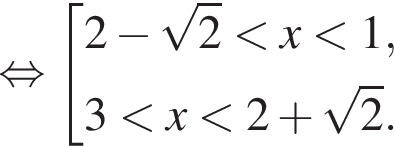
Для таких
Найдем решения второго неравенства системы с учетом ограничений на 
Прежде докажем неравенства 
и 
Действительно,
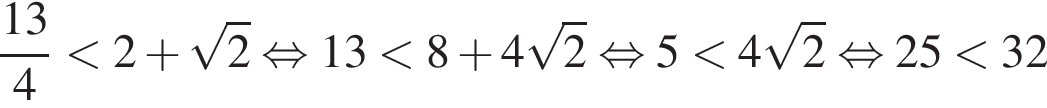(неравенство очевидное);
(неравенство очевидное).
Решения второго неравенства: 
Для получения пересечения решений обоих неравенств сравним числа 
и 
Докажем, что 
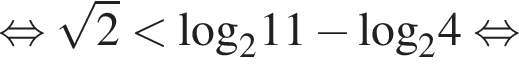
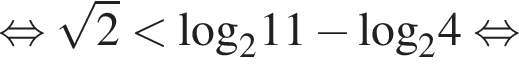
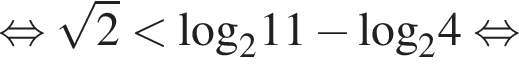
Левую часть последнего неравенства несколько увеличим, а правую же часть — уменьшим. Учитывая, что 
получим: 
(неравенство истинно). Итак,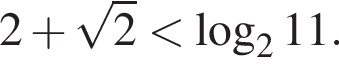 
Пересечением решений обоих неравенств будет множество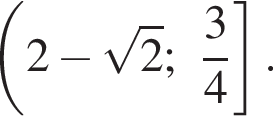 
Ответ: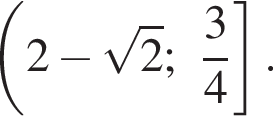
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Обоснованно получен верный ответ. | 3 |
| Обоснованно получены верные ответы в обоих неравенствах исходной системы. | 2 |
| Обоснованно получен верный ответ в одном неравенстве исходной системы. ИЛИ получен неверный ответ из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения системы неравенств. | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше. | 0 |
| Максимальный балл | 3 |