Тип Д13 C3 № 505980 
Классификатор алгебры: Неравенства, рациональные относительно логарифмической функции, Системы неравенств
Методы алгебры: Введение замены
Системы сложных неравенств. Системы, содержащие логарифмическое неравенство
i
Решите систему неравенств 
Решение. Рассмотрим первое неравенство системы:
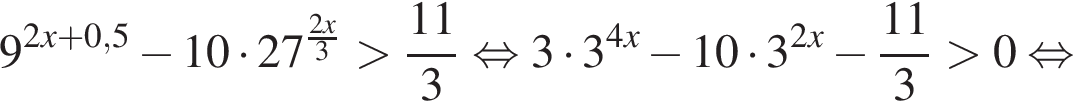
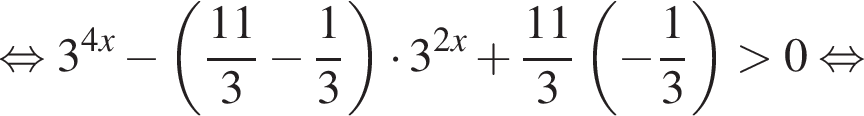
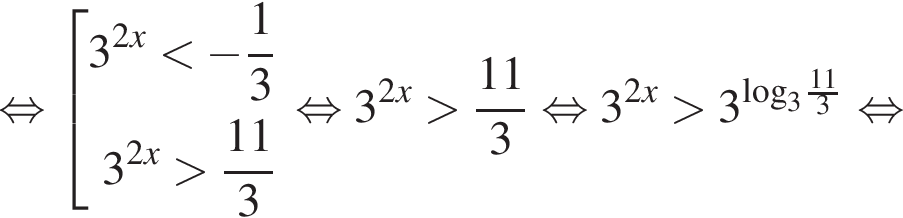
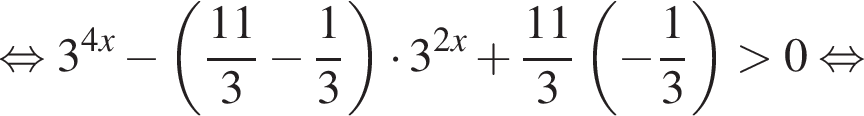
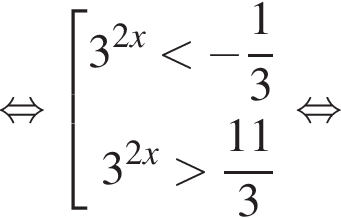
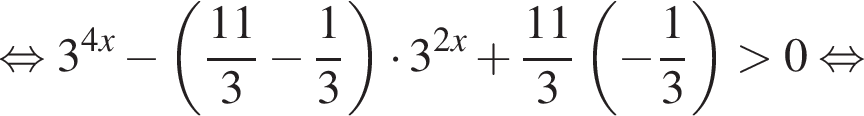
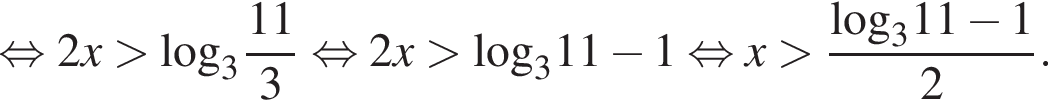
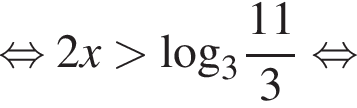
Теперь решим второе неравенство системы:
Введем новую переменную 
Тогда: 
Решим это неравенство методом интервалов:
Получили: 
А это значит:
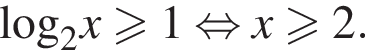
Таким образом, решениями второго неравенства системы является множество 
Прежде чем искать пресечение решений обоих неравенств системы, докажем неравенство 
(неравенство очевидное).
Таким образом, пересечением решений обоих неравенств системы является множество 
Ответ:
Критерии проверки:
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Обоснованно получен верный ответ. | 3 |
| Обоснованно получены верные ответы в обоих неравенствах исходной системы. | 2 |
| Обоснованно получен верный ответ в одном неравенстве исходной системы. ИЛИ получен неверный ответ из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения системы неравенств. | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше. | 0 |
| Максимальный балл | 3 |
Ответ:
505980
Классификатор алгебры: Неравенства, рациональные относительно логарифмической функции, Системы неравенств
Методы алгебры: Введение замены