Тип Д10 C2 № 505967 
Сложная стереометрия. Многогранники
i
В основании прямой призмы  лежит прямоугольный треугольник с острым углом А, равным 30°. Найдите площадь сечения призмы, проходящего через меньший катет BC одного основания и середину гипотенузы
лежит прямоугольный треугольник с острым углом А, равным 30°. Найдите площадь сечения призмы, проходящего через меньший катет BC одного основания и середину гипотенузы  противоположного основания призмы, если расстояние между основаниями призмы равно расстоянию от вершины А до искомого сечения и равно 6.
противоположного основания призмы, если расстояние между основаниями призмы равно расстоянию от вершины А до искомого сечения и равно 6.
Решение. 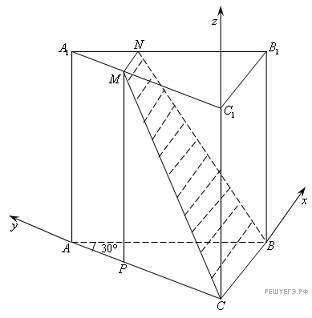 Пусть точка N — середина гипотенузы
Пусть точка N — середина гипотенузы  Построим заданное сечение (CMNB, M — середина отрезка
Построим заданное сечение (CMNB, M — середина отрезка  ), P — проекция точки M на плоскость нижнего основания призмы.
), P — проекция точки M на плоскость нижнего основания призмы.
Поместим призму в декартову систему координат, как показано на рисунке.
Составим уравнение плоскости  Поскольку сечение проходит через начало координат, значение d в уравнении
Поскольку сечение проходит через начало координат, значение d в уравнении  будет равно нулю. Сторона BC заданного треугольника лежит на оси
будет равно нулю. Сторона BC заданного треугольника лежит на оси  это значит, что в уравнении плоскости значение коэффициента а рано нулю. Итак, искомое уравнение будет иметь вид:
это значит, что в уравнении плоскости значение коэффициента а рано нулю. Итак, искомое уравнение будет иметь вид:  Пусть
Пусть  Тогда
Тогда 
Выпишем координаты необходимых точек: 

Для нахождения значений в и с достаточно подставить координаты точки M в уравнение 

Итак, искомое уравнение выглядит так:  Разделим обе части уравнения на
Разделим обе части уравнения на  Получим:
Получим:
 или
или 
Далее для вычисления значения m используем формулу расстояния от точки до плоскости.




 (не подходит по смыслу задачи).
(не подходит по смыслу задачи).
Итак, ВС = 4. Очевидно, что  (по свойству средней линии треугольника).
(по свойству средней линии треугольника). 

В прямоугольном треугольнике MPC  =
=
Для вычисления искомой площади заметим:
1)  — трапеция по способу построения и с учетом условия задачи.
— трапеция по способу построения и с учетом условия задачи.
2) MC — наклонная к (ABC), PC — проекция наклонной  следовательно,
следовательно,  по теореме о трех перпендикулярах.
по теореме о трех перпендикулярах.

Ответ: 
Критерии проверки:| Критерии оценивания выполнения задания | Баллы |
|---|
| Обоснованно получен верный ответ. | 2 |
| Решение содержит обоснованный переход к планиметрической задаче, но получен неверный ответ или решение не закончено ИЛИ при правильном ответе решение недостаточно обосновано. | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше. | 0 |
Ответ: 
лежит прямоугольный треугольник с острым углом А, равным 30°. Найдите площадь сечения призмы, проходящего через меньший катет BC одного основания и середину гипотенузы
противоположного основания призмы, если расстояние между основаниями призмы равно расстоянию от вершины А до искомого сечения и равно 6.
 PDF-версии:
PDF-версии: 