Решите систему неравенств: 
Решение. Найдем ограничения на x самой системы:
или 
Покажем, что
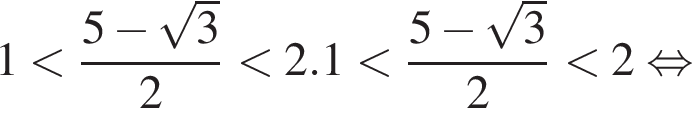
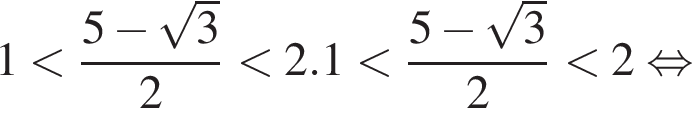
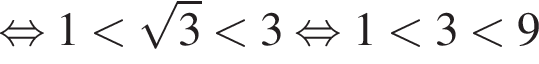(неравенство верно).
Очевидно, что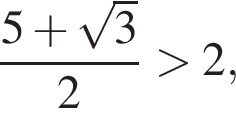 
поскольку 
Итак, получаем ограничения на x: 
Рассмотрим первое неравенство системы:
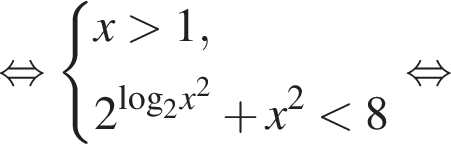
С учетом разрешенных значений x получим решения первого неравенства системы: 
Теперь решим второе неравенство системы на множестве разрешенных значений x методом рационализации:
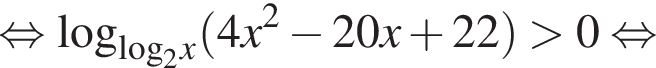
Заметим, что при всех значениях 
решения первого неравенства системы — справедливы неравенства 
Следовательно,
на указанном множестве. Тогда на этом же множестве решения неравенства (*) есть множество 
Для получения окончательного результата докажем неравенство 
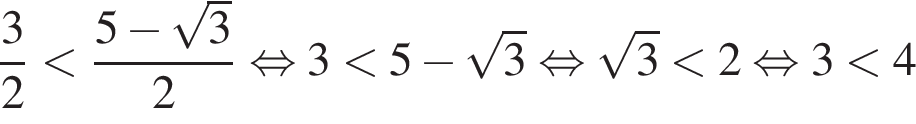(неравенство очевидное).
Пресечение ранее полученных результатов с решениями второго неравенства будет множество 
Ответ:
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Обоснованно получен верный ответ. | 3 |
| Обоснованно получены верные ответы в обоих неравенствах исходной системы. | 2 |
| Обоснованно получен верный ответ в одном неравенстве исходной системы. ИЛИ получен неверный ответ из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения системы неравенств. | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше. | 0 |
| Максимальный балл | 3 |