i
В бесконечной возрастающей последовательности натуральных чисел каждое делится хотя бы на одно из чисел 1005 и 1006 , но ни одно не делится на 97. Кроме того, каждые два соседних числа отличаются не более, чем на k. При каком наименьшем k такое возможно?
при некотором натуральном 
Тогда найдется такое n, что 
но 
(при этом 
из условия). Но наибольшими числами, меньшими D и делящимися на 1005 и 1006, являются числа 
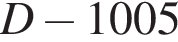и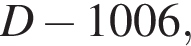 
соответственно; поэтому 
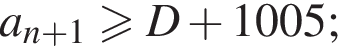отсюда 
подходит, например, последовательность всех чисел, кратных 1005, но не кратных 97 (заметим, что 1005 не кратно 97).