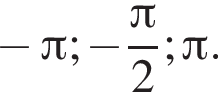Тип Д8 C1 № 505652 

Классификатор алгебры: Тригонометрические уравнения, Тригонометрические уравнения, сводимые к целым на синус или косинус
Методы алгебры: Замена — сумма или разность, Тригонометрические формулы суммы и разности функций
Уравнения, системы уравнений. Сложные тригонометрические уравнения
i
а) Решите уравнение 
б) Найдите все корни на промежутке 
Решение. a) 

Пусть 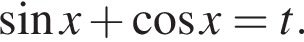 Тогда
Тогда

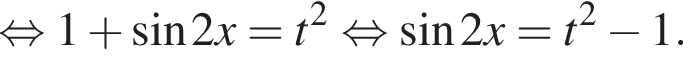



В таком случае заданное уравнение примет вид:  решим данное уравнение:
решим данное уравнение:



Теперь перейдем к переменной ![]()











Уравнение 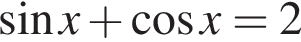 решений не имеет. В противном случае синус и косинус одного и того же аргумента обязаны равняться единице, что невозможно.
решений не имеет. В противном случае синус и косинус одного и того же аргумента обязаны равняться единице, что невозможно.
б) Отберём корни. Из серии 


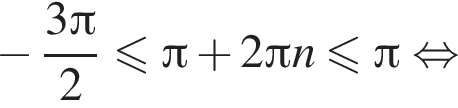


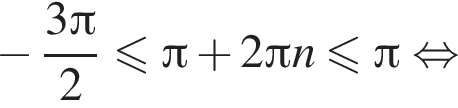



При 
 при
при 
Из серии 









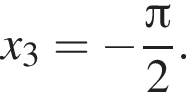
Ответ: а)  б)
б) 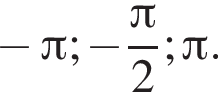
Критерии проверки:
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Обоснованно получены верные ответы в обоих пунктах. | 2 |
| Обоснованно получен верный ответ в пункте а, или в пункте б. ИЛИ получены неверные ответы из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения обоих пунктов — пункта а и пункта б. | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше. | 0 |
| Максимальный балл | 2 |
Ответ: а)  б)
б) 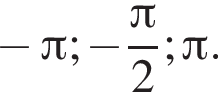
 б)
б) 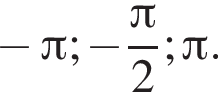
505652
а)  б)
б) 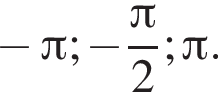
 б)
б)