Тип Д15 C4 № 505637 
Сложная планиметрия. Окружности
i
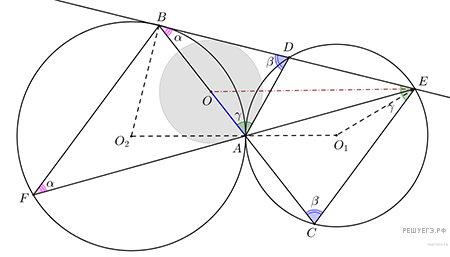
Две окружности касаются друг друга внешним образом в точке A. Прямая, проходящая через точку A, пересекает первую окружность в точке B, а вторую — в точке C. Касательная к первой окружности, проходящая через точку B, пересекает вторую окружность в точках D и E (D лежит между B и E). Известно, что AB = 5, AC = 4. Точка O — центр окружности, касающейся отрезка AD и продолжений отрезков ED и EA за точки D и A соответственно.
а) Докажите, что 
б) Найдите длину отрезка CE.
Решение. Центр вписанной в угол окружности лежит на биссектрисе угла. Для решения задачи докажем следующую лемму.
Лемма: точка O принадлежит стороне AB, то есть AB является биссектрисой угла DAF.
Доказательство: во-первых, из свойств секущих к окружности получим:

Тогда треугольники ABD и EBC подобны (угол ABD общий). Тогда ∠BDA = ∠BCE = β, ∠BAD = ∠BEC = γ.
Во-вторых, угол между дугой и касательной равен вписанному углу, опирающемуся на данную хорду, откуда ∠BFA = ∠ABD = α.
Далее, центральный угол AO2B в 2 раза больше вписанного угла AFB, поэтому  Так как треугольник AO2B равнобедренный (AO2 = O2B = R1), то
Так как треугольник AO2B равнобедренный (AO2 = O2B = R1), то

Аналогично для угла ACE:

Углы  и
и  равны, как вертикальные, и потому получаем:
равны, как вертикальные, и потому получаем:

Отсюда получаем, что  а значит точка O лежит на стороне AB. Лемма доказана.
а значит точка O лежит на стороне AB. Лемма доказана.
Из леммы получили:



Тогда  и треугольники AEC и EBC подобны по 2-м углам, откуда выпишем соотношения:
и треугольники AEC и EBC подобны по 2-м углам, откуда выпишем соотношения:

Из равенства первой и третьей дробей получим:

Тогда 
Проведем дополнительно отрезок EO — он является биссектрисой угла BEA, а значит и биссектрисой треугольника ABE. Тогда по свойству биссектрисы в треугольнике имеем:

Требуемое доказано.
Ответ: 6.
Критерии проверки:| Критерии оценивания выполнения задания | Баллы |
|---|
| Имеется верное доказательство утверждения пункта а и обоснованно получен верный ответ в пункте б. | 3 |
| Получен обоснованный ответ в пункте б. ИЛИ Имеется верное доказательство утверждения пункта а и при обоснованном решении пункта б получен неверный ответ из-за арифметической ошибки. | 2 |
| Имеется верное доказательство утверждения пункта а. ИЛИ При обоснованном решении пункта б получен неверный ответ из-за арифметической ошибки. ИЛИ Обоснованно получен верный ответ в пункте б и использованием утверждения пункта а, при этом пункт а не выполнен. | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше. | 0 |
| Максимальный балл | 3 |
Ответ: 6.
 PDF-версии:
PDF-версии: 