Найдите все значения a, при которых уравнение 
на промежутке 
имеет ровно два корня.
Решение. Рассмотрим функции 
и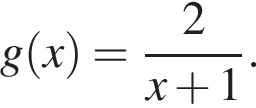 
Исследуем 
на промежутке 
При 
все значения функции 
на промежутке неположительны, а все значения функции 
— положительны, поэтому при уравнение не имеет решений на промежутке
При 
функция возрастает на промежутке 
Функция убывает на этом промежутке, поэтому уравнение всегда имеет ровно одно решение на промежутке поскольку 
а 
На промежутке 
уравнение принимает вид 
Это уравнение сводится к уравнению 
Будем считать, что 
поскольку случай был рассмотрен ранее. Дискриминант квадратного уравнения 
поэтому при 
это уравнение не имеет корней; при 
уравнение имеет единственный корень, равный 2; при 
уравнение имеет два корня.
Пусть уравнение имеет два корня, то есть 
Тогда оба корня меньше 5, поскольку при 
значения функции 
неположительны, а значения функции 
положительны. По теореме Виета сумма корней равна 4, а произведение равно 
Значит, больший корень всегда принадлежит промежутку 
а меньший принадлежит этому промежутку тогда и только тогда, когда 
Таким образом, уравнение имеет следующее количество корней на промежутке :
1) Нет корней при 
2) Один корень при 
3) Два корня при и 
4) Три корня при 
Ответ: 
Решим данную задачу графически.
Построим графики функций 
и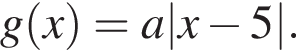 
на промежутке График функции представляет собой часть гиперболы, график функции — график функции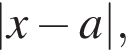 
растягиваемый в a раз.
Из графика видно, что при 
решений нет. Ровно два решения возможно, когда является касательной к в некоторой точке H (cм. рис.), соответственно второе решение — пересечение и в точке H1. Поэтому:
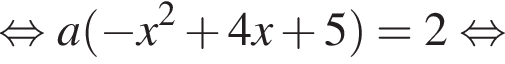
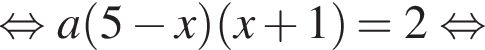
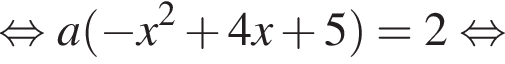
Поскольку в точке H необходимо касание, то у квадратного уравнения 
дискриминант должен быть равен нулю. 
По условию 
не подходит. Таким образом, до 
и 
уравнение имеет либо 0, либо 3 решения.
Стоит отметить, что при 
функция будет пересекать в точке (0; 2) и, следовательно, будет 3 решения. Найдем значение a, при котором будет три пересечения на промежутке : 
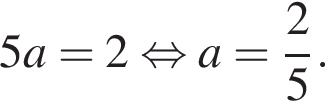Тогда при 
будет всего два решения, поскольку будет всего два пересечения.
Ответ:
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Обоснованно получен верный ответ | 4 |
| С помощью верного рассуждения получено множество значений а, отличающееся от искомого конечным числом точек | 3 |
| С помощью верного рассуждения получены все граничные точки искомого множества значений а | 2 |
| Верно получена хотя бы одна граничная точка искомого множества значений а | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 4 |