1. Тип 13 № 519423 

Классификатор алгебры: Рациональные уравнения
Методы алгебры: Введение замены
Кодификатор ФИПИ/Решу ЕГЭ: 2.1.2 Рациональные уравнения
Уравнения. Рациональные уравнения
i
а) Решите уравнение 
б) Найдите его корни, принадлежащие отрезку 
Решение. а) Сделаем замену  возведём обе части в квадрат:
возведём обе части в квадрат:


![]()


тогда  Имеем:
Имеем:






Вернемся к исходной переменной. Если  то
то









Если ![]() то
то









б) Выясним, какие из найденных корней принадлежат отрезку  В силу неравенств
В силу неравенств
 и
и 
из найденных корней уравнения заданному отрезку принадлежат только числа ![]() и
и 
Ответ: а)  б)
б) 
Критерии проверки:
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Обоснованно получены верные ответы в обоих пунктах. | 2 |
| Обоснованно получен верный ответ в пункте а), ИЛИ получены неверные ответы из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения пункта а) и пункта б). | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше. | 0 |
| Максимальный балл | 2 |
Ответ: а)  б)
б) 
 б)
б) 
519423
а)  б)
б) 
 б)
б) 
Классификатор алгебры: Рациональные уравнения
Методы алгебры: Введение замены
Кодификатор ФИПИ/Решу ЕГЭ: 2.1.2 Рациональные уравнения


 тогда
тогда  Имеем:
Имеем: 

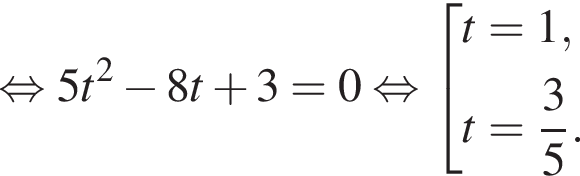




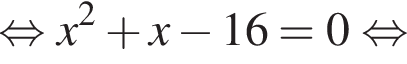
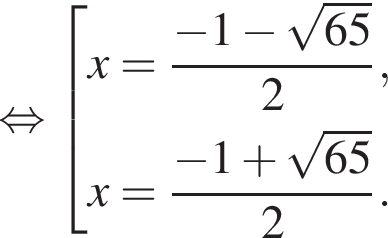





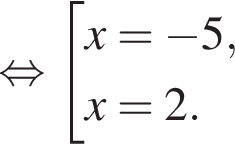
 Положительные корни не могут лежать в этом отрезке. Число –5 лежит в нем. Корень
Положительные корни не могут лежать в этом отрезке. Число –5 лежит в нем. Корень  тоже лежит в этом отрезке в силу цепочки соотношений:
тоже лежит в этом отрезке в силу цепочки соотношений:



 б)
б) 



 тогда
тогда  Имеем:
Имеем: 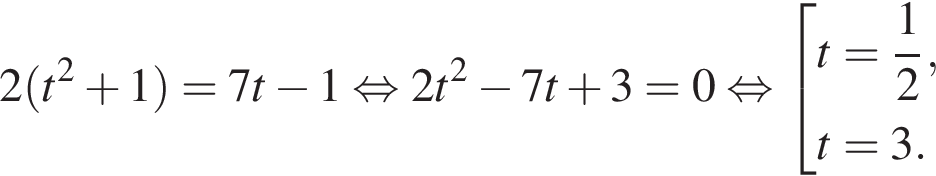



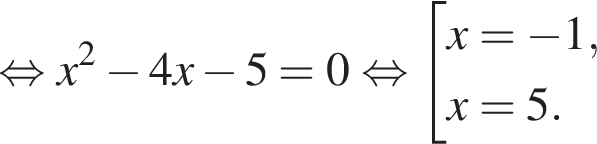










 В силу неравенств
В силу неравенств 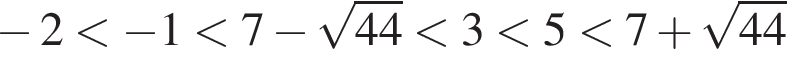

 б)
б) 


 Заметим, что
Заметим, что  а значит, уравнение записывается в виде
а значит, уравнение записывается в виде 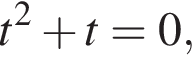 откуда
откуда  или
или 




 Подходят
Подходят  б)
б) 

 отбросим знаменатели, затем применим формулу разности квадратов:
отбросим знаменатели, затем применим формулу разности квадратов:

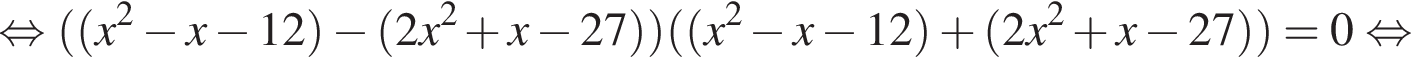





 Кроме того,
Кроме того,





 следовательно, подходит только x = 3.
следовательно, подходит только x = 3. б) x = 3.
б) x = 3.