1. Тип 13 № 633979 

Классификатор алгебры: Уравнения смешанного типа, Тригонометрические уравнения, Основное тригонометрическое тождество и его следствия
Методы алгебры: Использование основного тригонометрического тождества и следствий из него
Уравнения. Тригонометрия и логарифмы
i
а) Решите уравнение 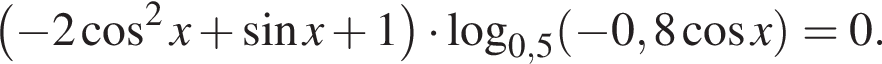
б) Найдите все корни уравнения, принадлежащие отрезку 
Решение. а) Уравнение определено, если аргумент логарифма положителен, то есть если 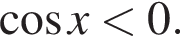 При этом условии уравнение эквивалентно совокупности:
При этом условии уравнение эквивалентно совокупности:


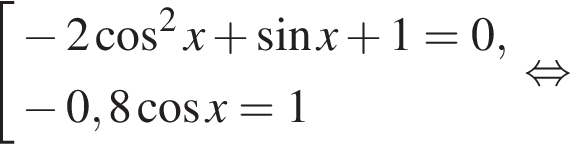


выше для решения уравнения мы использовали следствие из основного тригонометрического тождества: 
б) Отберем корни, лежащие на отрезке  при помощи двойного неравенства:
при помощи двойного неравенства:

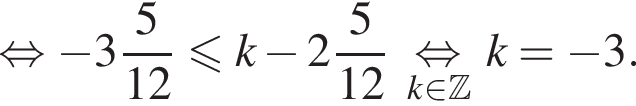



Найденному значению k соответствует корень 
Ответ: а)  б)
б) 
Критерии проверки:
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Обоснованно получены верные ответы в обоих пунктах. | 2 |
| Обоснованно получен верный ответ в пункте а), ИЛИ получены неверные ответы из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения пункта а) и пункта б). | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше. | 0 |
| Максимальный балл | 2 |
Ответ: а)  б)
б) 
 б)
б) 
633979
а)  б)
б) 
 б)
б) 


 Таким образом,
Таким образом,

 а значит,
а значит, 







 то есть
то есть 
 млн руб.
млн руб. млн руб.
млн руб.






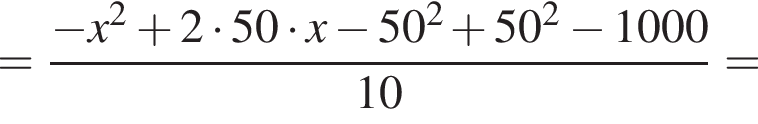

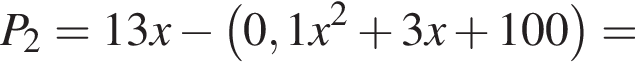
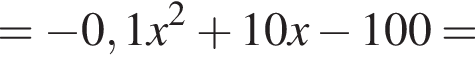

 млн руб.,
млн руб.,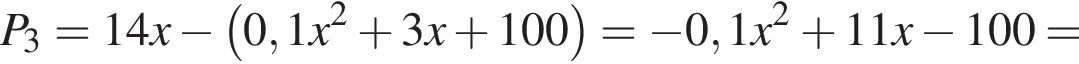





 млн руб.,
млн руб.,

 и
и 
 Основания KL и CD параллельны, поэтому
Основания KL и CD параллельны, поэтому








 тогда
тогда  и
и  Пусть отрезок LH — высота трапеции KCDL, следовательно,
Пусть отрезок LH — высота трапеции KCDL, следовательно, 
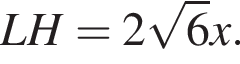 Тогда
Тогда 




 то есть
то есть 

 Тогда
Тогда 
 и
и  Находим основание BC:
Находим основание BC:





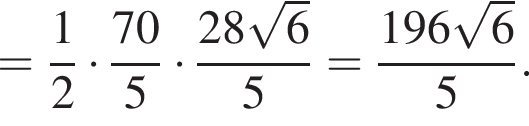


 тогда
тогда  и
и 



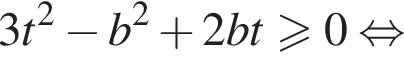


 монотонна на множестве действительных чисел при любом положительном значении a (при
монотонна на множестве действительных чисел при любом положительном значении a (при  возрастает, при
возрастает, при  тогда и только тогда, когда одновременно
тогда и только тогда, когда одновременно  и
и  откуда получаем:
откуда получаем: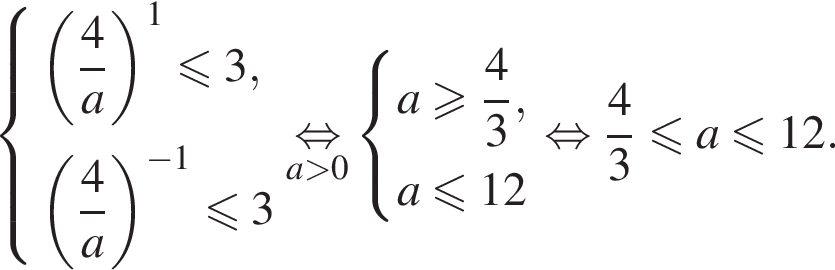



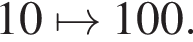
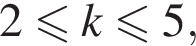 первая цифра числа обязательно меняется (если число было
первая цифра числа обязательно меняется (если число было  где
где  Тогда
Тогда 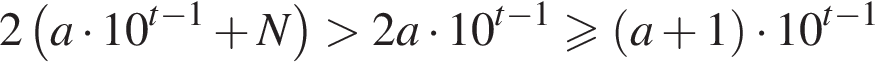
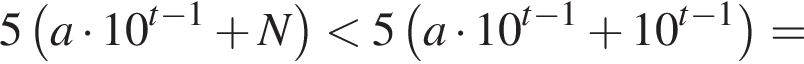




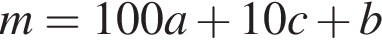 и
и  откуда
откуда  или
или  что возможно при a = 1, c = 0 и b = 8, то есть для варианта
что возможно при a = 1, c = 0 и b = 8, то есть для варианта