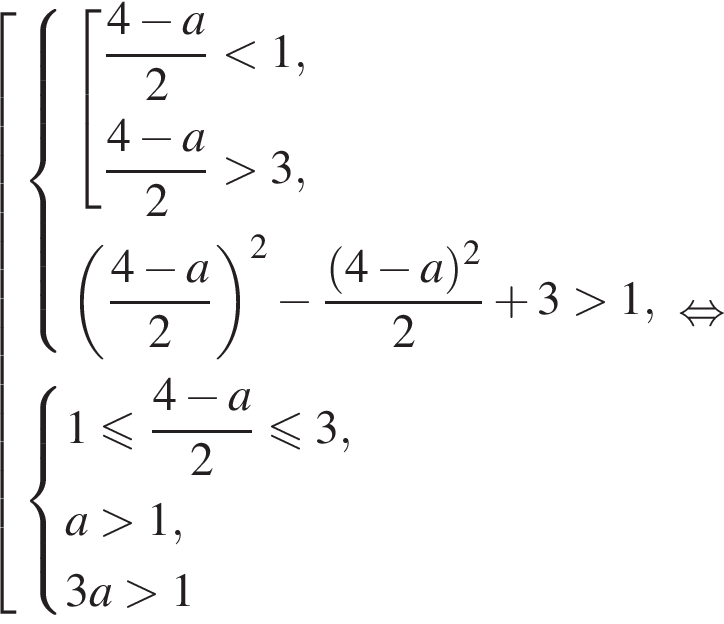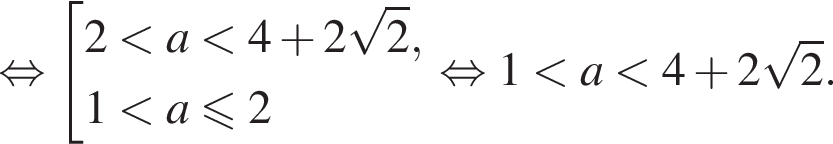1. Тип 13 № 561193 

Классификатор алгебры: Логарифмические уравнения, Область определения уравнения, Показательные уравнения, Тригонометрические уравнения, Уравнения смешанного типа
Методы алгебры: Замена переменной
Кодификатор ФИПИ/Решу ЕГЭ:
Уравнения. Другие уравнения смешанного типа
i
а) Решите уравнение 
б) Укажите корни этого уравнения, принадлежащие отрезку 
Решение. а) При условии
 и
и  исходное уравнение сводится к квадратному относительно показательной функции:
исходное уравнение сводится к квадратному относительно показательной функции:

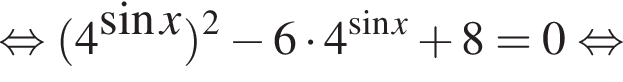



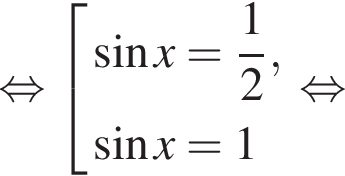

Условию равносильности удовлетворяет только серия 
б) Отберём корни при помощи единичной окружности (см. рис.). Подходит только ![]()
Ответ: а)  б)
б) ![]()
Критерии проверки:
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Обоснованно получены верные ответы в обоих пунктах. | 2 |
| Обоснованно получен верный ответ в пункте а), ИЛИ получены неверные ответы из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения пункта а) и пункта б). | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше. | 0 |
| Максимальный балл | 2 |
Ответ: а)  б)
б) 
 б)
б) 561193
а)  б)
б) 
 б)
б) Классификатор алгебры: Логарифмические уравнения, Область определения уравнения, Показательные уравнения, Тригонометрические уравнения, Уравнения смешанного типа
Методы алгебры: Замена переменной
Кодификатор ФИПИ/Решу ЕГЭ:



 откуда
откуда



 Из прямоугольных треугольников NBB1 и BON вычислим квадрат длины отрезка BN двумя способами, получим равенство:
Из прямоугольных треугольников NBB1 и BON вычислим квадрат длины отрезка BN двумя способами, получим равенство: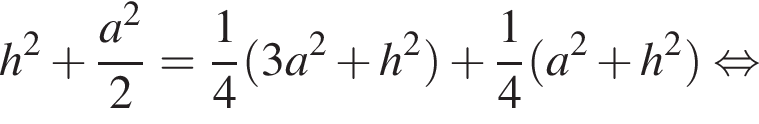


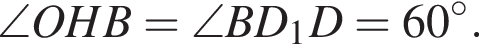

 и
и  тогда
тогда





















 Составим таблицу.
Составим таблицу.




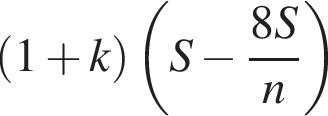





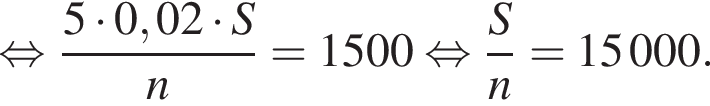


 значит,
значит, 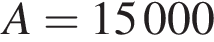 руб.
руб.







 руб.
руб.

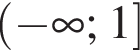 и
и  график функции представляет собой параболу, ветви которой направлены вверх. На отрезке [1; 3] график функции представляет собой параболу, ветви которой направлены вниз. Наименьшее значение функции достигается либо на краях отрезка [1; 3] или в вершине параболы, ветви которой направлены вверх, то есть в одной из трёх точек
график функции представляет собой параболу, ветви которой направлены вверх. На отрезке [1; 3] график функции представляет собой параболу, ветви которой направлены вниз. Наименьшее значение функции достигается либо на краях отрезка [1; 3] или в вершине параболы, ветви которой направлены вверх, то есть в одной из трёх точек 
 при условии
при условии  Для выполнения условия задачи должен быть выполнен один из двух случаев:
Для выполнения условия задачи должен быть выполнен один из двух случаев: