i
В треугольнике АВС на сторонах АВ и ВС отмечены точки М и N соответственно, причем ВМ = ВN. Через точку М проведена прямая, перпендикулярная ВС, а через точку N — прямая, перпендикулярная АВ. Эти прямые пересекаются в точке О. Продолжение отрезка ВО пересекает сторону АС в точке Р, АР = 5, РС = 4.
а) Докажите, что ВР — биссектриса треугольника АВС.
б) Найдите длину отрезка ВР, если ВС = 6.
Треугольник BMN — равнобедренный по определению, поэтому 
Значит, 
треугольник OMN — равнобедренный, то есть 
Следовательно, треугольники MBO и NBO равны по трем сторонам, откуда 
Таким образом, луч BP — биссектриса угла ABC.
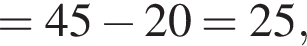
Тогда по теореме косинусов в треугольнике ABP:
