Дан остроугольный треугольник ABC. Известно, что 
Точка O — центр описанной окружности треугольника ABC. Вокруг треугольника AOC описана окружность, которая пересекает сторону BC в точке P.
а) Докажите, что треугольники ABC и PAC подобны.
б) Найдите AB, если BC = 6 и AC = 4.
Решение.
а) Пусть угол ABC равен α. Центральный угол COA и вписанный угол CBA опираются на одну дугу, значит, угол COA равен 2α. Вписанные в меньшую окружность углы COA и CPA опираются на одну дугу, следовательно, они равны. Тогда углы CPA и BAC равны 2α. Треугольники ABC и PAC с общим углом C подобны по двум углам.
б) Поскольку треугольники ABC и PAC подобны, то угол OAC равен углу ABC, то есть равен α. Тогда отрезок AP — биссектриса. Из подобия треугольников находим, что 
откуда
По свойству биссектрисы 
тогда
Ответ: б) 5.
Приведем решение пункта б) Александра Турбанова (Липецк).
По теореме синусов в треугольнике ABC 
откуда
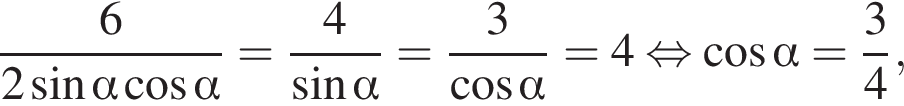
а потому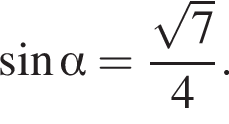 
Далее последовательно получаем:
Заметим, что 
поэтому
Итак, по теореме косинусов в треугольнике ABC:
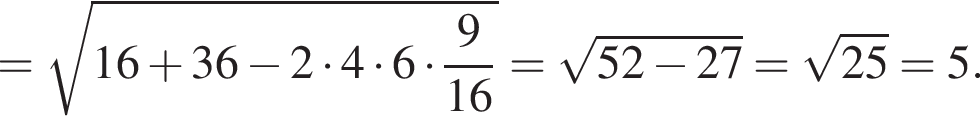
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Имеется верное доказательство утверждения пункта а), и обоснованно получен верный ответ в пункте б) | 3 |
| Получен обоснованный ответ в пункте б) ИЛИ имеется верное доказательство утверждения пункта а), и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | 2 |
| Имеется верное доказательство утверждения пункта а), ИЛИ при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки, ИЛИ обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | 1 |
| Решение не соответствует ни одному из критериев, приведённых выше | 0 |
| Максимальный балл | 3 |