Точки P, Q, W делят стороны выпуклого четырехугольника ABCD в отношении
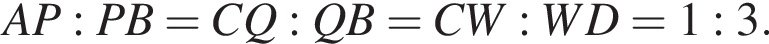
В треугольнике PQW угол W острый, радиус описанной вокруг него окружности 
а) Докажите, что треугольник PQW — прямоугольный.
б) Найдите площадь четырёхугольника ABCD.
Решение. а) По теореме синусов в треугольнике PQW имеем
следовательно,
отсюда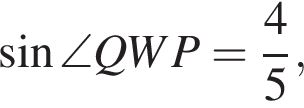 
Таким образом,
Следовательно, 
откуда, учитывая, что угол PWQ острый, находим, что 
и, значит, 
—
то есть 
Отсюда следует, что треугольник PQW — прямоугольный.
б) Треугольники ABC и PBQ подобны с коэффициентом подобия 
Отсюда следует, что отрезки PQ и AC параллельны и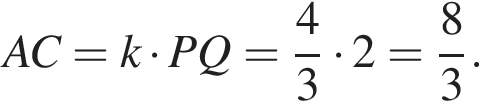 
Аналогично, отрезки QW и BD параллельны и BD = 6. Угол между прямыми AC и BD равен углу между прямыми PQ и QW. Угол между диагоналями четырёхугольника ABCD прямой. Поэтому его площадь равна
Ответ: б) 8.
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Имеется верное доказательство утверждения пункта а), и обоснованно получен верный ответ в пункте б) | 3 |
| Получен обоснованный ответ в пункте б) ИЛИ имеется верное доказательство утверждения пункта а), и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | 2 |
| Имеется верное доказательство утверждения пункта а), ИЛИ при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки, ИЛИ обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | 1 |
| Решение не соответствует ни одному из критериев, приведённых выше | 0 |
| Максимальный балл | 3 |