i
B правильной четырёхугольной призме ABCDA1B1C1D1 сторона AB основания равна 5, а боковое ребро AA1 ![]()
а) Докажите, что прямая A1C перпендикулярна плоскости γ.
б) Найдите объём пирамиды, вершина которой — точка A1, а основание сечение данной призмы плоскостью γ.


 Пусть продолжение прямой PQ за точку Q пересекает продолжение прямой CC1 за точку C1 в точке T. Треугольник AA1C подобен треугольнику CPT, поскольку
Пусть продолжение прямой PQ за точку Q пересекает продолжение прямой CC1 за точку C1 в точке T. Треугольник AA1C подобен треугольнику CPT, поскольку
 и треугольники AA1C и HPC подобны, а значит, угол PHC — прямой. Прямые A1C и PT перпендикулярны, прямая A1C перпендикулярна прямой BD, следовательно, (по признаку перпендикулярности прямой и плоскости), прямая A1C перпендикулярна плоскости γ.
и треугольники AA1C и HPC подобны, а значит, угол PHC — прямой. Прямые A1C и PT перпендикулярны, прямая A1C перпендикулярна прямой BD, следовательно, (по признаку перпендикулярности прямой и плоскости), прямая A1C перпендикулярна плоскости γ.
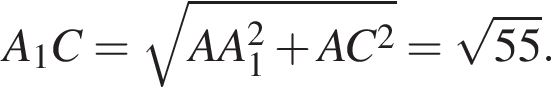
 Следовательно,
Следовательно,  Объём пирамиды A1KNLM равен
Объём пирамиды A1KNLM равен 
