РЕШУ ЕГЭ — математика профильная

Задания

Тип 13 № 660397 Добавить в вариант

Источник: А. Ларин. Тренировочный вариант № 468

Классификатор алгебры: Уравнения смешанного типа, Тригонометрические уравнения, сводимые к целым на тангенс или котангенс

Методы алгебры: Формулы двойного угла

Уравнения. Тригонометрические уравнения, разные задачи

а)  Решите уравнение $корень из: начало аргумента: 3 конец аргумента синус 2 x минус 3 косинус в квадрате x = косинус x умножить на e в степени левая круглая скобка натуральный логарифм левая круглая скобка минус косинус x правая круглая скобка правая круглая скобка .$

б)  Найдите все корни уравнения, принадлежащие отрезку $левая квадратная скобка минус дробь: числитель: 3 Пи , знаменатель: 4 конец дроби ; 4 Пи правая квадратная скобка .$

Решение. а)  Уравнение определено при $косинус x меньше 0.$ При этом условии справедливо тождество $e в степени левая круглая скобка натуральный логарифм левая круглая скобка минус косинус x правая круглая скобка правая круглая скобка = минус косинус x,$ откуда получаем:

$корень из: начало аргумента: 3 конец аргумента синус 2 x минус 3 косинус в квадрате x = минус косинус в квадрате x равносильно$
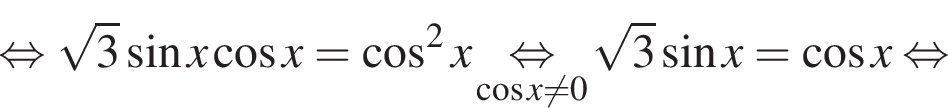
$равносильно корень из: начало аргумента: 3 конец аргумента синус x косинус x = косинус в квадрате x \underset косинус x не равно 0 \mathop равносильно корень из: начало аргумента: 3 конец аргумента синус x = косинус x равносильно$
$равносильно \ctg x = корень из 3 равносильно x= дробь: числитель: Пи , знаменатель: 6 конец дроби плюс Пи k, \underset косинус x меньше 0 \mathop равносильно x= дробь: числитель: 7 Пи , знаменатель: 6 конец дроби плюс 2 Пи k, k принадлежит Z .$ $корень из: начало аргумента: 3 конец аргумента синус 2 x минус 3 косинус в квадрате x = минус косинус в квадрате x равносильно$
$равносильно корень из: начало аргумента: 3 конец аргумента синус x косинус x = косинус в квадрате x \underset косинус x не равно 0 \mathop равносильно$
$\mathop равносильно корень из: начало аргумента: 3 конец аргумента синус x = косинус x равносильно \ctg x = корень из 3 равносильно$
$равносильно x= дробь: числитель: Пи , знаменатель: 6 конец дроби плюс Пи k, \underset косинус x меньше 0 \mathop равносильно x= дробь: числитель: 7 Пи , знаменатель: 6 конец дроби плюс 2 Пи k, k принадлежит Z .$ $корень из: начало аргумента: 3 конец аргумента синус 2 x минус 3 косинус в квадрате x = минус косинус в квадрате x равносильно$
$равносильно корень из: начало аргумента: 3 конец аргумента синус x косинус x = косинус в квадрате x \underset косинус x не равно 0 \mathop равносильно$
$\mathop равносильно корень из: начало аргумента: 3 конец аргумента синус x = косинус x равносильно$
$равносильно \ctg x = корень из 3 равносильно x= дробь: числитель: Пи , знаменатель: 6 конец дроби плюс Пи k, \underset косинус x меньше 0 \mathop равносильно$
$\mathop равносильно x= дробь: числитель: 7 Пи , знаменатель: 6 конец дроби плюс 2 Пи k, k принадлежит Z .$ $корень из: начало аргумента: 3 конец аргумента синус 2 x минус 3 косинус в квадрате x = минус косинус в квадрате x равносильно$
$равносильно корень из: начало аргумента: 3 конец аргумента синус x косинус x = косинус в квадрате x \underset косинус x не равно 0 \mathop равносильно$
$\mathop равносильно корень из: начало аргумента: 3 конец аргумента синус x = косинус x равносильно$
$равносильно \ctg x = корень из 3 равносильно$
$равносильно x= дробь: числитель: Пи , знаменатель: 6 конец дроби плюс Пи k, \underset косинус x меньше 0 \mathop равносильно$
$\mathop равносильно x= дробь: числитель: 7 Пи , знаменатель: 6 конец дроби плюс 2 Пи k, k принадлежит Z .$

б)  Отберем корни при помощи двойного неравенства:

$минус дробь: числитель: 3 Пи , знаменатель: 4 конец дроби меньше или равно дробь: числитель: 7 Пи , знаменатель: 6 конец дроби плюс 2 Пи k меньше или равно 4 Пи равносильно минус дробь: числитель: 23, знаменатель: 24 конец дроби меньше или равно k меньше или равно дробь: числитель: 17, знаменатель: 12 конец дроби равносильно совокупность выражений k = 0, k = 1. конец совокупности .$ $минус дробь: числитель: 3 Пи , знаменатель: 4 конец дроби меньше или равно дробь: числитель: 7 Пи , знаменатель: 6 конец дроби плюс 2 Пи k меньше или равно 4 Пи равносильно$
$равносильно минус дробь: числитель: 23, знаменатель: 24 конец дроби меньше или равно k меньше или равно дробь: числитель: 17, знаменатель: 12 конец дроби равносильно совокупность выражений k = 0, k = 1. конец совокупности .$

Найденным значениям k соответствуют корни $дробь: числитель: 7 Пи , знаменатель: 6 конец дроби ,$ $дробь: числитель: 19 Пи , знаменатель: 6 конец дроби .$

Ответ: a) $левая фигурная скобка дробь: числитель: 7 Пи , знаменатель: 6 конец дроби плюс 2 Пи k : k принадлежит Z правая фигурная скобка ;$ б) $дробь: числитель: 7 Пи , знаменатель: 6 конец дроби ,$ $дробь: числитель: 19 Пи , знаменатель: 6 конец дроби .$

Критерии проверки:

Критерии оценивания выполнения задания	Баллы
Обоснованно получены верные ответы в обоих пунктах	2
Обоснованно получен верный ответ в пункте а), ИЛИ получены неверные ответы из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения пункта а) и пункта б)	1
Решение не соответствует ни одному из критериев, перечисленных выше	0
Максимальный балл	2

660397

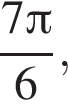
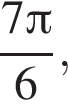
a) $левая фигурная скобка дробь: числитель: 7 Пи , знаменатель: 6 конец дроби плюс 2 Пи k : k принадлежит Z правая фигурная скобка ;$ б) $дробь: числитель: 7 Пи , знаменатель: 6 конец дроби ,$ $дробь: числитель: 19 Пи , знаменатель: 6 конец дроби .$

Источник: А. Ларин. Тренировочный вариант № 468

Методы алгебры: Формулы двойного угла

Ключ

№ п/п	№ задания	Ответ
1	660397	a) $левая фигурная скобка дробь: числитель: 7 Пи , знаменатель: 6 конец дроби плюс 2 Пи k : k принадлежит Z правая фигурная скобка ;$ б) $дробь: числитель: 7 Пи , знаменатель: 6 конец дроби ,$ $дробь: числитель: 19 Пи , знаменатель: 6 конец дроби .$