РЕШУ ЕГЭ — математика профильная

Задания

Участники конкурса на лучшую математическую задачу анонимно присылают каждый свою задачу. После публикации все участники дают оценку каждой задаче, кроме своей. В конкурсе принимают участие 6 человек. Каждый участник за лучшую по его мнению задачу дает 5 баллов, за следующую  — 4 балла и так далее, за пятую  — 1 балл. По каждой задаче баллы суммируются, так определяется рейтинг задачи.

а)  Могут ли все рейтинги быть простыми числами?

б)   Могла ли сумма четырех наибольших рейтингов быть в три раза больше суммы остальных?

в)  Какова минимальная сумма третьего и четвертого рейтингов, если им дали номера в порядке невозрастания?

Решение. Заметим сразу, что сумма рейтингов от каждого участника это 15, поэтому общая сумма рейтингов равна 90. Кроме того, будем считать, что каждый оценил и свою задачу тоже, в 0 баллов.

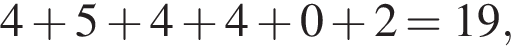а)  Да, это возможно. Пусть эксперты выставили такие оценки (по порядку, от первого до шестого): за первую задачу $5 плюс 4 плюс 5 плюс 5 плюс 4 плюс 0=23,$ за вторую задачу $4 плюс 5 плюс 4 плюс 4 плюс 0 плюс 2=19,$ за третью задачу $3 плюс 2 плюс 3 плюс 0 плюс 5 плюс 4=17,$ за четвертую задачу $2 плюс 3 плюс 0 плюс 3 плюс 2 плюс 3=13,$ за пятую задачу $1 плюс 0 плюс 2 плюс 2 плюс 3 плюс 5=13,$ за шестую задачу $0 плюс 1 плюс 1 плюс 1 плюс 1 плюс 1=5.$ Нетрудно убедиться, что каждый эксперт выставил все оценки по разу.

б)  Пусть сумма двух наименьших равна x, тогда сумма остальных равна 3x, поэтому общая сумма рейтингов равна $x плюс 3x=4x=90,$ откуда x нецелое.

в)  Заметим, что сумма первого и второго рейтинга не более $5 плюс 5 плюс 5 плюс 5 плюс 5 плюс 5 плюс 4 плюс 4 плюс 4 плюс 4=46,$ поэтому сумма остальных рейтингов не менее 90 − 46  =  44. Ясно, что сумма третьего и четвертого не меньше чем сумма двух последних, значит, она не меньше половины оставшихся баллов, откуда наименьшее значение не меньше 22. Пример для 22 построить можно: за первую задачу $5 плюс 5 плюс 5 плюс 5 плюс 5 плюс 0=25,$ за вторую задачу $4 плюс 4 плюс 4 плюс 4 плюс 0 плюс 5=21,$ за третью задачу $1 плюс 1 плюс 2 плюс 0 плюс 3 плюс 4=11,$ за четвертую задачу $3 плюс 2 плюс 0 плюс 1 плюс 4 плюс 1=11,$ за пятую задачу $2 плюс 0 плюс 1 плюс 3 плюс 2 плюс 3=11,$ за шестую задачу $0 плюс 3 плюс 3 плюс 2 плюс 1 плюс 2=11.$

Ответ: а)  да; б)  нет; в)  22.

Критерии оценивания выполнения задания	Баллы
Верно получены все перечисленные (см. критерий на 1 балл) результаты	4
Верно получены три из перечисленных (см. критерий на 1 балл) результатов	3
Верно получены два из перечисленных (см. критерий на 1 балл) результатов	2
Верно получен один из следующий результатов: ―  обоснованное решение в п. а; ―  пример в п. б; ―  искомая оценка в п. в; ―  пример в п. в, обеспечивающий точность предыдущей оценки	1
Решение не соответствует ни одному из критериев, перечисленных выше	0
Максимальный балл	4

№ п/п	№ задания	Ответ
1	623663	а)  да; б)  нет; в)  22.

Ключ