i
Числа 1, 2, 3, 4, 5, 6, 7, 8, 9, 16 произвольно делят на три группы так, чтобы в каждой группе было хотя бы одно число. Затем вычисляют значение среднего арифметического чисел в каждой из групп (для группы из единственного числа среднее арифметическое равно этому числу).
а) Могут ли быть одинаковыми два из этих трех значений средних арифметических в группах из разного количества чисел?
б) Могут ли быть одинаковыми все три значения средних арифметических?
в) Найдите наименьшее возможное значение наибольшего из получаемых трех средних арифметических
Однако эта дробь несократима, поэтому для равенства ей какого-то из средних требуется взять не менее 10 чисел. Значит, в каждой группе должно быть не менее 10 чисел, что невозможно.
где 
(поскольку на остальные две группы должно прийтись не менее двух чисел). Из всех таких дробей наименьшей будет 
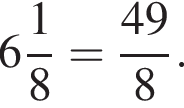Но тогда на оставшиеся две группы приходятся два числа с суммой 12 и среднее в одной из групп будет не меньше 7.
Тогда на остальные две группы приходятся три числа с суммой 18. Это можно реализовать, взяв в одну группу 6, а в другую 5 и 7. Тогда в этих группах среднее составит 6, а в третьей, состоящей из остальных чисел, 