РЕШУ ЕГЭ — математика профильная

Задания

Тип 15 № 548802 Добавить в вариант

Источники:

ЕГЭ по математике 24.07.2020. Основная волна, резервный день;

Задания 15 ЕГЭ–2020.

Классификатор алгебры: Показательные уравнения и неравенства, Показательные уравнения, свойства степени

Методы алгебры: Введение замены, Группировка, Метод интервалов, Сведение к однородному

Неравенства. Показательные неравенства

Решите неравенство $3 умножить на 45 в степени x минус 3 умножить на 27 в степени x минус 28 умножить на 15 в степени x плюс 28 умножить на 9 в степени x плюс 9 умножить на 5 в степени x минус 3 в степени левая круглая скобка x плюс 2 правая круглая скобка \leqslant0.$

Решение. Cгруппируем и разложим на множители:

$равносильно 3 умножить на 45 в степени x минус 3 умножить на 27 в степени x минус 28 умножить на 15 в степени x плюс 28 умножить на 9 в степени x плюс 9 умножить на 5 в степени x минус 9 умножить на 3 в степени x меньше или равно 0 равносильно$

$равносильно 3 умножить на 3 в степени левая круглая скобка 2x правая круглая скобка левая круглая скобка 5 в степени x минус 3 в степени x правая круглая скобка минус 28 умножить на 3 в степени x левая круглая скобка 5 в степени x минус 3 в степени x правая круглая скобка плюс 9 левая круглая скобка 5 в степени x минус 3 в степени x правая круглая скобка меньше или равно 0 равносильно$

$равносильно левая круглая скобка 5 в степени x минус 3 в степени x правая круглая скобка левая круглая скобка 3 умножить на 3 в степени левая круглая скобка 2x правая круглая скобка минус 28 умножить на 3 в степени x плюс 9 правая круглая скобка меньше или равно 0.$

Решим уравнение $5 в степени x минус 3 в степени x =0.$ Получаем:

$5 в степени x = 3 в степени x равносильно левая круглая скобка дробь: числитель: 5, знаменатель: 3 конец дроби правая круглая скобка в степени x = 1 равносильно x = 0.$

Решим уравнение $3 умножить на 3 в степени левая круглая скобка 2x правая круглая скобка минус 28 умножить на 3 в степени x плюс 9 = 0.$ Положим $t = 3 в степени x ,$ получим уравнение $3t в квадрате минус 28t плюс 9 = 0,$ откуда $t = дробь: числитель: 1, знаменатель: 3 конец дроби$ или $t = 9.$ Тогда $3 в степени x = дробь: числитель: 1, знаменатель: 3 конец дроби$ или $3 в степени x = 9,$ откуда $x= минус 1$ или $x=2.$

Итак, левая часть обращается в нуль в точках −1, 0 и 2. Для решения неравенства применим метод интервалов, находим $x меньше или равно минус 1$ или $0 меньше или равно x меньше или равно 2.$

Ответ: $левая круглая скобка минус бесконечность ; минус 1 правая квадратная скобка \cup левая квадратная скобка 0; 2 правая квадратная скобка .$

Приведем другое решение.

Cгруппируем и разложим на множители:

$3 умножить на 45 в степени x минус 3 умножить на 27 в степени x минус 28 умножить на 15 в степени x плюс 28 умножить на 9 в степени x плюс 9 умножить на 5 в степени x минус 3 в степени левая круглая скобка x плюс 2 правая круглая скобка меньше или равно 0 равносильно$

$равносильно левая круглая скобка 3 умножить на 3 в степени левая круглая скобка 2x правая круглая скобка минус 28 умножить на 3 в степени x плюс 9 правая круглая скобка левая круглая скобка 5 в степени x минус 3 в степени x правая круглая скобка меньше или равно 0 равносильно$
$равносильно левая круглая скобка 3 умножить на 3 в степени x минус 1 правая круглая скобка левая круглая скобка 3 в степени x минус 9 правая круглая скобка левая круглая скобка 5 в степени x минус 3 в степени x правая круглая скобка меньше или равно 0 равносильно$

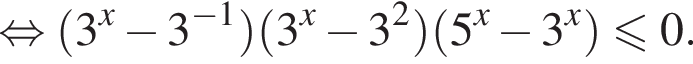
$равносильно левая круглая скобка 3 в степени x минус 3 в степени левая круглая скобка минус 1 правая круглая скобка правая круглая скобка левая круглая скобка 3 в степени x минус 3 в квадрате правая круглая скобка левая круглая скобка 5 в степени x минус 3 в степени x правая круглая скобка меньше или равно 0.$

Применим метод рационализации: заменим каждый множитель на рациональный, имеющий с ним тот же знак. Получаем:

$левая круглая скобка x минус левая круглая скобка минус 1 правая круглая скобка правая круглая скобка левая круглая скобка x минус 2 правая круглая скобка x меньше или равно 0 равносильно$
$равносильно левая круглая скобка x плюс 1 правая круглая скобка левая круглая скобка x минус 2 правая круглая скобка x меньше или равно 0 равносильно совокупность выражений x меньше или равно минус 1,0 меньше или равно x меньше или равно 2. конец совокупности .$ $левая круглая скобка x минус левая круглая скобка минус 1 правая круглая скобка правая круглая скобка левая круглая скобка x минус 2 правая круглая скобка x меньше или равно 0 равносильно$
$равносильно левая круглая скобка x плюс 1 правая круглая скобка левая круглая скобка x минус 2 правая круглая скобка x меньше или равно 0 равносильно$
$равносильно совокупность выражений x меньше или равно минус 1,0 меньше или равно x меньше или равно 2. конец совокупности .$

Критерии проверки:

Критерии оценивания выполнения задания	Баллы
Обоснованно получен верный ответ	2
Обоснованно получен ответ, отличающийся от верного исключением точек, ИЛИ получен неверный ответ из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения	1
Решение не соответствует ни одному из критериев, перечисленных выше.	0
Максимальный балл	2

548802

$левая круглая скобка минус бесконечность ; минус 1 правая квадратная скобка \cup левая квадратная скобка 0; 2 правая квадратная скобка .$

Источники:

ЕГЭ по математике 24.07.2020. Основная волна, резервный день;

Задания 15 ЕГЭ–2020.

Классификатор алгебры: Показательные уравнения и неравенства, Показательные уравнения, свойства степени

Методы алгебры: Введение замены, Группировка, Метод интервалов, Сведение к однородному

Ключ

№ п/п	№ задания	Ответ
1	548802	$левая круглая скобка минус бесконечность ; минус 1 правая квадратная скобка \cup левая квадратная скобка 0; 2 правая квадратная скобка .$