Найдите все значения параметра a, при каждом из которых уравнение
имеет ровно два различных корня.
Решение. Уравнение определено на множестве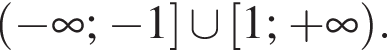 
Пусть 
тогда, чтобы исходное уравнение имело два различных корня, необходимо и достаточно, чтобы уравнение
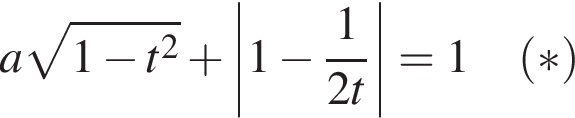
имело ровно одно решение при 
Рассмотрим два случая раскрытия модуля.
1 случай. Если 
то имеем:
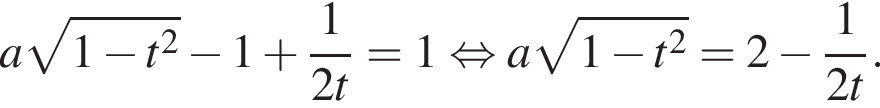
Построим эскизы графиков левой и правой частей полученного уравнения в системе координат 
График левой части — дуга эллипса, при 
вырождающаяся в отрезок. График правой части — гипербола. Уравнение имеет одно решение при 
и не имеет решений при 
где 
— значение параметра, при котором график функции 
проходит через точку 
Найдём значение :
2 случай. Если 
то имеем:
Построим эскизы графиков левой и правой частей уравнения в системе координат
График левой части — дуга эллипса, при вырождающаяся в отрезок. График правой части — гипербола. Найдем количество точек пересечения дуги эллипса с гиперболой:
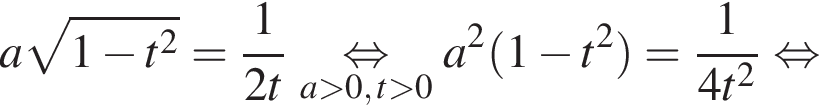
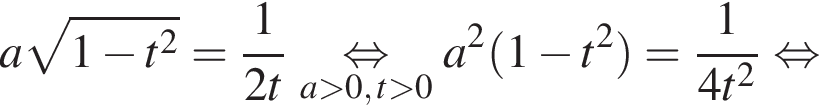
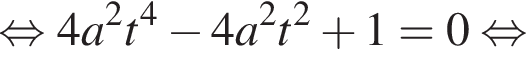
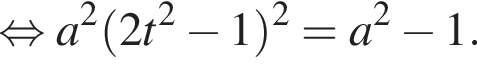
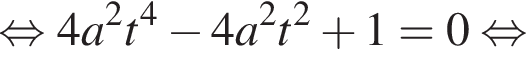
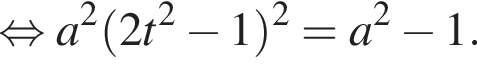
Единственному положительному корню соответствуют значения 
С учётом условия 
получаем, что искомое значение параметра 
Тогда уравнение не имеет решений при 
имеет одно решение при 
или 
имеет два решения при 
где — проходит через точку
Объединяя два случая, получаем, что для 
уравнение (⁎) при 
имеет при одно решение, при 
— два решения, при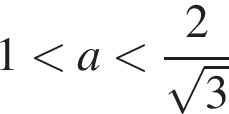 
— три решения, при 
— два решения, при 
— одно решение.
Ответ: 
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Обоснованно получен правильный ответ | 4 |
| С помощью верного рассуждения получен ответ, но в решении допущена вычислительная ошибка или оно недостаточно обосновано | 3 |
| С помощью верного рассуждения получен ответ, но в ходе решения допущена одна ошибка, отличная от вычислительной | 2 |
| Получены некоторые верные значения параметра, однако решение содержит более одной ошибки | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |