Основание прямой призмы 
равнобедренный треугольник ABC, в котором 
Высота призмы равна 
На сторонах 
и AC выбраны соответственно точки 
и D так, что 
и через эти точки проведена плоскость.
а) Найдите площадь сечения призмы этой плоскостью.
б) Найдите расстояние от точки 
до плоскости сечения.
Решение. Пусть H и
— середины ребер AC и 
соответственно. Тогда 
и по теореме Пифагора
а) Заметим, что 
— средняя линия треугольника 
поэтому прямая перпендикулярна прямой 
Проведем тогда через D прямую, перпендикулярную AC, она будет параллельна 
поэтому тоже будет лежать в плоскости сечения. Плоскость сечения пересекает еще ребро 
и сечения является пятиугольником. Спроецируем его на плоскость нижнего основания. Площадь полученного пятиугольника можно найти, вычитая из площади ABC две площади прямоугольных треугольников. У одного катет 
и гипотенуза
поэтому второй катет 
и площадь 
У другого катет 
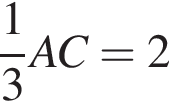и он подобен первому по двум углам, коэффициент подобия равен 
Значит, его площадь равна 
Итого, площадь проекции равна
Найдем теперь угол между плоскостью основания и плоскостью сечения. Плоскости пересекаются по прямой, проведенной через D перпендикулярно AC. Значит, AC и 
— перпендикуляры к этой прямой (второе- по теореме о трех перпендикулярах, его проекция лежит на AC). Осталось посчитать угол между ними. Ясно что 
— гипотенуза треугольника с вертикальным катетом 
(высота призмы) и горизонтальным
поэтому
и 
По теореме о площади фигуры и площади проекции, площадь сечения равна: 
б) Проведем из высоту к 
Она будет перпендикулярна к по построению и к поскольку будет лежать в грани 
перпендикулярной к 
Значит, эта высота будет перпендикулярна двум пересекающимся прямым плоскости сечения, поэтому она-то и даст расстояние от точки до плоскости. Получаем:
Ответ: а) 
б) 
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Обоснованно получен верный ответ. | 2 |
| Решение содержит обоснованный переход к планиметрической задаче, но получен неверный ответ или решение не закончено ИЛИ при правильном ответе решение недостаточно обосновано. | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше. | 0 |
б) б)