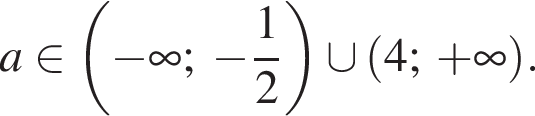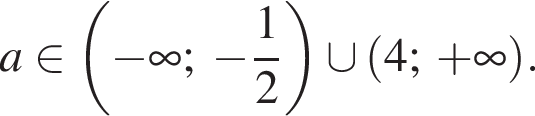Найдите все значения a, при каждом из которых наименьшее значение функции

меньше −2.
Решение. При  модуль раскрывается «со знаком минус»:
модуль раскрывается «со знаком минус»:  На отрезке [1; 3] график функции представляет собой параболу, ветви которой направлены вниз.
На отрезке [1; 3] график функции представляет собой параболу, ветви которой направлены вниз.
При ![]() или
или ![]() модуль раскрывается «со знаком плюс»:
модуль раскрывается «со знаком плюс»:  График функции на этих лучах представляет собой параболу, ветви которой направлены вверх. Вершина этой параболы может лежать левее отрезка [1; 3], правее этого отрезка или на самом отрезке. Рассмотрим эти случаи.
График функции на этих лучах представляет собой параболу, ветви которой направлены вверх. Вершина этой параболы может лежать левее отрезка [1; 3], правее этого отрезка или на самом отрезке. Рассмотрим эти случаи.
Если ![]() и
и  то есть если
то есть если



то наименьшее значение функции достигается в вершине, абсцисса которой ![]() Оно равно:
Оно равно:






По условию требуется, чтобы наименьшее значение было меньше −2:
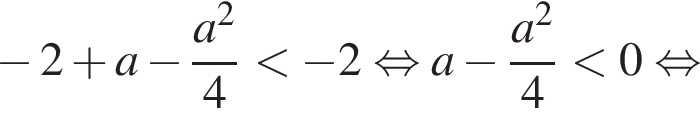








С учетом того, что  получаем:
получаем: 
Осталось рассмотреть случай, когда вершина параболы, ветви которой направлены вверх, лежит на отрезке [1; 3]. В этом случае параметр  а наименьшее значение функции достигается на концах отрезка. Найдем
а наименьшее значение функции достигается на концах отрезка. Найдем  и
и  Наименьшее значение функции может быть меньше −2, только если
Наименьшее значение функции может быть меньше −2, только если  то есть при
то есть при 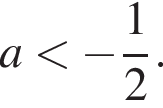 Учитывая ограничения на a, получаем:
Учитывая ограничения на a, получаем: 
Объединяя найденные значения параметра, получаем ответ: 
Приведем другое решение.
Заданная функция непрерывна и на бесконечностях стремится к плюс бесконечности. Поэтому при любом значении параметра она достигает своего наименьшего значения. Тогда для того, чтобы наименьшее значение функции  было меньше −2, необходимо и достаточно, чтобы неравенство
было меньше −2, необходимо и достаточно, чтобы неравенство  имело решение. Запишем его в виде
имело решение. Запишем его в виде

и построим графики левой и правой частей неравенства.
График левой части неравенства — парабола (см. рис.), пересекающая ось абсцисс в точках 1 и 3, с отражённой относительно оси абсцисс отрицательной частью. График правой части неравенства — пучок прямых, проходящих через точку (1; −1).
Нетрудно заметить, что неравенство имеет решения, когда графики имеют более одной точки пересечения. То есть когда прямая проходит выше точки (3; 0) или выше точки касания с параболой на луче (−∞; 1].
В первом случае угловой коэффициент ![]() прямой
прямой  должен быть больше углового коэффициента прямой, проходящей через точку (3; 0). Имеем:
должен быть больше углового коэффициента прямой, проходящей через точку (3; 0). Имеем: 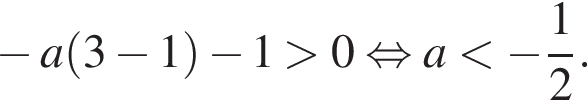
Во втором случае запишем уравнение  в виде
в виде  и найдем дискриминант полученного квадратного уравнения:
и найдем дискриминант полученного квадратного уравнения: 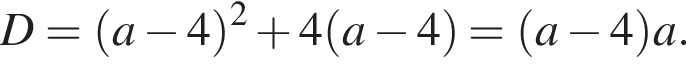 Парабола имеет с касательной единственную общую точку, поэтому касанию соответствует дискриминант, равный нулю, откуда a = 0 или a = 4. Подходит только положительный корень, соответствующий отрицательному угловому коэффициенту прямой.
Парабола имеет с касательной единственную общую точку, поэтому касанию соответствует дискриминант, равный нулю, откуда a = 0 или a = 4. Подходит только положительный корень, соответствующий отрицательному угловому коэффициенту прямой.
Таким образом, получаем ответ: 
Ответ: 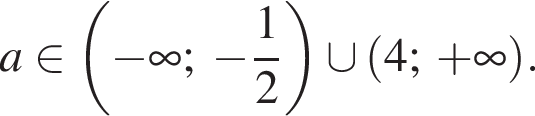
Примечание Льва Бреслава (Санкт-Петербург).
Во втором решении ссылка на то, что функция непрерывна и на бесконечностях стремится к плюс бесконечности является существенной. Например, для внешне очень похожей функции 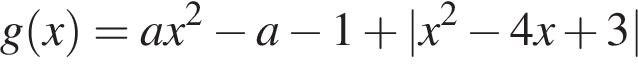 аналогичная переформулировка не будет равносильна изначальной задаче.
аналогичная переформулировка не будет равносильна изначальной задаче.
Примечание редакции Решу ЕГЭ.
Полностью соглашаясь с предыдущим замечанием, отметим, что на ЕГЭ снижать оценку ученику за отсутствие указанного обоснования неправильно. Смоленская комиссия ЕГЭ в 2019 году оценила второе решение одним баллом из четырёх, объяснив на апелляции, что решающий должен явно показать, что рассматриваемая им функция достигает наименьшего значения. Работа была перепроверена Рособрнадзором, принявшим решение о выставлении полного балла. Подробности этой истории подробно описаны Дмитрием Гущиным здесь, ряд интересных комментариев есть здесь.
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Обоснованно получен правильный ответ. | 4 |
| С помощью верного рассуждения получены все значения a, но в ответ ошибочно включены одна или обе граничные точки. | 3 |
| С помощью верного рассуждения получены не все значения a. | 2 |
| Задача верно сведена к исследованию взаимного расположения графика функции и прямой (аналитически или графически). | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше. | 0 |