РЕШУ ЕГЭ — математика профильная

Задания

В школах № 1 и № 2 учащиеся писали тест. Из каждой школы тест писали по крайней мере два учащихся, а суммарно тест писал 51 учащийся. Каждый учащийся, писавший тест, набрал натуральное количество баллов. Оказалось, что в каждой школе средний балл был целым числом. После этого один из учащихся, писавших тест, перешел из школы № 1 в школу № 2, а средние баллы за тест были пересчитаны в обеих школах.

а)  Мог ли средний балл в школе № 1 вырасти в два раза?

б)  Средний балл в школе № 1 вырос на 10%, средний балл в школе № 2 также вырос на 10%. Мог ли первоначальный средний балл в школе № 2 равняться 1?

в)  Средний балл в школе № 1 вырос на 10%, средний балл в школе № 2 также вырос на 10%. Найдите наименьшее значение первоначального среднего балла в школе № 2.

Решение. а)  Пусть в школе № 1 писали тест n учащихся, а средний балл был равен А. Тогда суммарный балл всех учащихся этой школы равнялся nA. После перехода учащегося в школу № 2 средний балл вырос в два раза, то есть стал равен 2A, а количество учащихся стало $n минус 1.$ Тогда суммарный балл после перехода учащегося стал равен $2 левая круглая скобка n минус 1 правая круглая скобка A.$ Таким образом, суммарный балл уменьшился на $nA минус 2 левая круглая скобка n минус 1 правая круглая скобка A = левая круглая скобка 2 минус n правая круглая скобка A,$ что невозможно, поскольку перешедший учащийся набрал положительное количество баллов, а $n\geqslant2.$

б)  Пусть в школе № 2 средний балл равнялся В, а перешедший в нее учащийся набрал u баллов. Тогда получаем:

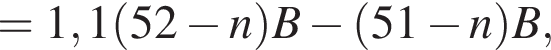
$u=nA минус 1,1 левая круглая скобка n минус 1 правая круглая скобка A=1,1 левая круглая скобка 52 минус n правая круглая скобка B минус левая круглая скобка 51 минус n правая круглая скобка B,$ $u=nA минус 1,1 левая круглая скобка n минус 1 правая круглая скобка A=$
$=1,1 левая круглая скобка 52 минус n правая круглая скобка B минус левая круглая скобка 51 минус n правая круглая скобка B,$

или

$10u= левая круглая скобка 11 минус n правая круглая скобка A= левая круглая скобка 62 минус n правая круглая скобка B.$

Если $B=1,$ то $n=2,$ поскольку число $левая круглая скобка 62 минус n правая круглая скобка B$ должно делиться на 10, а $левая круглая скобка 11 минус n правая круглая скобка A$ не должно быть отрицательным. Получаем $9A=60,$ что невозможно, поскольку A целое.

в)  Заметим, что если $B=2,$ то $n=2$ или $n=7.$ В первом случае $9A=120,$ а во втором $4A=110.$ Значит, ни один из этих случаев не возможен.

При $B=3$ получаем $n=2,$ откуда $u=18,$ $A=20.$ Этот случай реализуется, например, если в школе № 1 писали тест 2 учащихся и набрали 22 и 18 баллов, а в школе № 2 писали тест 49 учащихся и каждый набрал по три балла, а у перешедшего из одной школы в другую учащегося 18 баллов.

Ответ: а)  нет; б)  нет; в)  3.

Критерии оценивания выполнения задания	Баллы
Верно получены все перечисленные (см. критерий на 1 балл) результаты.	4
Верно получены три из перечисленных (см. критерий на 1 балл) результатов.	3
Верно получены два из перечисленных (см. критерий на 1 балл) результатов.	2
Верно получен один из следующий результатов: ―  обоснованное решение в п. а; ―  пример в п. б; ―  искомая оценка в п. в; ―  пример в п. в, обеспечивающий точность предыдущей оценки.	1
Решение не соответствует ни одному из критериев, перечисленных выше.	0
Максимальный балл	4

№ п/п	№ задания	Ответ
1	520808	а)  нет; б)  нет; в)  3.

Ключ