Ре­ше­ние. а)  Тре­уголь­ник AOH рав­но­бед­рен­ный и тра­пе­ция ABCD рав­но­бед­рен­ная, по­это­му ∠AHO = ∠OAH = ∠CDA. Зна­чит, пря­мые OH и CD па­рал­лель­ны, а так как OQ  — сред­няя линия тра­пе­ции, то па­рал­лель­ны пря­мые OQ и AD. Про­ти­во­по­лож­ные сто­ро­ны четырёхуголь­ни­ка DQOH по­пар­но па­рал­лель­ны, сле­до­ва­тель­но, DQOH  — па­рал­ле­ло­грамм.

б)  Пусть окруж­ность с цен­тром в точке O ра­ди­у­са R ка­са­ет­ся сто­ро­ны CD в точке P. В пря­мо­уголь­ных тре­уголь­ни­ках OPQ и AHB имеем

По­это­му

Пусть AH  =  x. По­сколь­ку тра­пе­ция ABCD рав­но­бед­рен­ная, AD  =  2AH + BC, DH  =  AH + BC  =  x + 2. Тогда

от­ку­да Зна­чит,

Ответ: б) 

При­ве­дем ре­ше­ние пунк­та б) Доб­ры­ни Мер­ку­рье­ва.

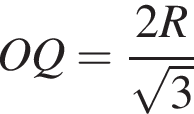Из пунк­та а) из­вест­но, что и что OQ  — сред­няя линия тра­пе­ции. Сле­до­ва­тель­но, Тре­уголь­ник AOH  — рав­но­бед­рен­ный, AH  =  R. В па­рал­ле­ло­грам­ме про­ти­во­по­лож­ные сто­ро­ны равны: HD  =  OQ. Кроме того 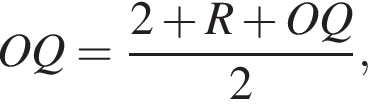то есть По­лу­ча­ем:

Таким об­ра­зом,