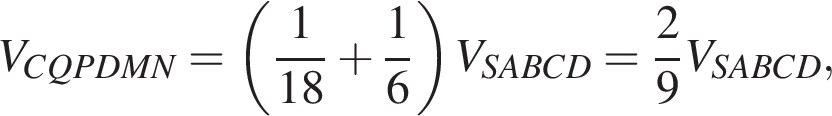i
Дана правильная четырёхугольная пирамида SABCD с вершиной S. Точка M расположена на SD так, что SM : SD = 2 : 3. P — середина ребра AD, а Q — середина ребра BC.
а) Докажите, что сечение пирамиды плоскостью MQP — равнобедренная трапеция.
б) Найдите отношение объёмов многогранников, на которые плоскость MQP разбивает пирамиду.
поэтому PDCQ — параллелограмм, 
поэтому 
то есть 
Так как 
и 
так как пирамида правильная, то 
следовательно, 
и 
то MNQP — равнобедренная трапеция, что и требовалось доказать.
расстояние от точки M до плоскости ABC втрое меньше расстояния от точки S до плоскости ABC. Тогда 
расстояние от точки D до плоскости SBC в 1,5 раза больше, чем от точки M. Значит, 
из чего следует, что 
