РЕШУ ЕГЭ — математика профильная

Задания

Тип 18 № 514538 Добавить в вариант

Источник: ЕГЭ по математике 06.06.2016. Основная волна

Классификатор алгебры: Уравнения с параметром

Методы алгебры: Перебор случаев, Перебор случаев

Задача с параметром. Уравнения с параметром, содержащие радикалы

Найдите все значения а, при каждом из которых уравнение

$корень из: начало аргумента: x в степени 4 минус 9x в квадрате плюс a в квадрате конец аргумента =x в квадрате минус 3x минус a$

имеет ровно три различных корня.

Решение. Возводя в квадрат, получаем

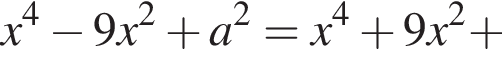
$x в степени 4 минус 9x в квадрате плюс a в квадрате =x в степени 4 плюс 9x в квадрате плюс a в квадрате минус 6x в кубе минус 2ax в квадрате плюс 6ax,$ $x в степени 4 минус 9x в квадрате плюс a в квадрате =x в степени 4 плюс 9x в квадрате плюс$
$плюс a в квадрате минус 6x в кубе минус 2ax в квадрате плюс 6ax,$

то есть

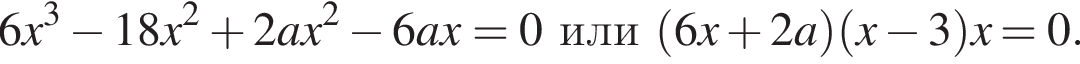
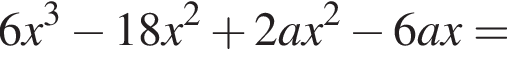
$6x в кубе минус 18x в квадрате плюс 2ax в квадрате минус 6ax=0или левая круглая скобка 6x плюс 2a правая круглая скобка левая круглая скобка x минус 3 правая круглая скобка x=0.$ $6x в кубе минус 18x в квадрате плюс 2ax в квадрате минус 6ax=$
$=0или левая круглая скобка 6x плюс 2a правая круглая скобка левая круглая скобка x минус 3 правая круглая скобка x=0.$

Его корни 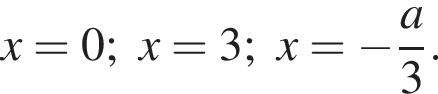$x=0;x=3;x= минус дробь: числитель: a, знаменатель: 3 конец дроби .$ Осталось узнать, не посторонние ли это корни, и все ли они различны (их как раз три).

При $x=0$ изначальное уравнение примет вид $корень из: начало аргумента: a в квадрате конец аргумента = минус a,$ что верно при $a меньше или равно 0.$

При $x=3$ изначальное уравнение примет вид $корень из: начало аргумента: a в квадрате конец аргумента = минус a,$ что верно при $a меньше или равно 0.$

При $x= минус дробь: числитель: a, знаменатель: 3 конец дроби$ изначальное уравнение примет вид $корень из: начало аргумента: a в степени 4 конец аргумента =a в квадрате ,$ что верно при при всех a.

Совпадение корней происходит при $a=0$ или $a= минус 9.$

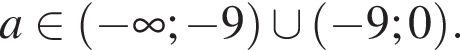
Ответ: $a принадлежит левая круглая скобка минус бесконечность ; минус 9 правая круглая скобка \cup левая круглая скобка минус 9;0 правая круглая скобка .$

Критерии проверки:

Критерии оценивания выполнения задания	Баллы
Обоснованно получен правильный ответ.	4
Найдено множество значений a, корни, соответствующие единственному значению параметра не определены ИЛИ Найдены корни, но в множество значений a не включены одна или две граничные точки.	3
Найдено множество значений a, но не включены одна или две граничные точки. Корни, соответствующие единственному значению параметра не найдены.	2
Верно найдена хотя бы одна граничная точка искомого множества значений a	1
Решение не соответствует ни одному из критериев, перечисленных выше.	0

514538

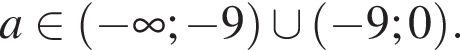
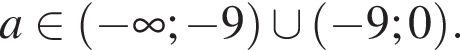
$a принадлежит левая круглая скобка минус бесконечность ; минус 9 правая круглая скобка \cup левая круглая скобка минус 9;0 правая круглая скобка .$

Источник: ЕГЭ по математике 06.06.2016. Основная волна

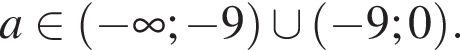
Классификатор алгебры: Уравнения с параметром

Методы алгебры: Перебор случаев, Перебор случаев

Ключ

№ п/п	№ задания	Ответ
1	514538	$a принадлежит левая круглая скобка минус бесконечность ; минус 9 правая круглая скобка \cup левая круглая скобка минус 9;0 правая круглая скобка .$