Ре­ше­ние. а)  Пусть O  — от­лич­ная от A₁ точка пе­ре­се­че­ния окруж­но­стей, опи­сан­ных около тре­уголь­ни­ков A₁CB₁ и A₁BC₁ (рис. 1).

Тогда

от­ку­да

Зна­чит, сле­до­ва­тель­но, точки A, B₁, O и C₁ лежат на одной окруж­но­сти.

б)  Пусть O₁, O₂ и O₃  — цен­тры окруж­но­стей, опи­сан­ных около тре­уголь­ни­ков B₁AC₁, A₁BC₁ и A₁CB₁ со­от­вет­ствен­но (рис. 2). За­ме­тим, что как ра­ди­у­сы опи­сан­ных окруж­но­стей около рав­ных тре­уголь­ни­ков. Зна­чит, тре­уголь­ни­ки AO₁C₁ и C₁O₂B равны. Кроме того, тре­уголь­ник O₂C₁O₁ также равен этим тре­уголь­ни­кам, по­сколь­ку

Таким об­ра­зом, Ана­ло­гич­но, 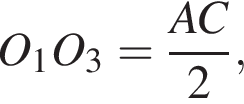по­это­му тре­уголь­ник O₁O₂O₃ по­до­бен тре­уголь­ни­ку ABC с ко­эф­фи­ци­ен­том и ра­ди­ус впи­сан­ной в него окруж­но­сти равен по­ло­ви­не ра­ди­у­са окруж­но­сти, впи­сан­ной в тре­уголь­ник ABC.

Пусть M  — се­ре­ди­на BC, а ра­ди­ус окруж­но­сти, впи­сан­ной в тре­уголь­ник ABC, равен r (рис. 3). Тогда пло­щадь тре­уголь­ни­ка ABC равна

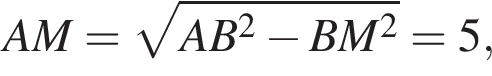C дру­гой сто­ро­ны, вы­со­та рав­но­бед­рен­но­го тре­уголь­ни­ка ABC равна по­это­му пло­щадь тре­уголь­ни­ка ABC равна 60. Зна­чит, r  =  2,4. Ис­ко­мый ра­ди­ус равен

Ответ: 1,2.