Тип Д15 C4 № 512468 
Сложная планиметрия. Треугольники
i
На основании AC равнобедренного треугольника ABC взята точка E. Окружности w1 и w2, вписанные в треугольники ABE и CBE, касаются прямой BE в точках K и M соответственно.
а) Докажите, что 
б) Определите, на сколько радиус окружности w2 больше радиуса окружности w1, если известно, что AE = 9, СЕ = 15, а радиус вписанной в треугольник ABC окружности равен 4.
Решение. а) Прежде решим вспомогательную задачу.
Задача: если в произвольном треугольнике ABC D — точка касания стороны AB и окружности, вписанной в этот треугольник, то верно равенство: 
(См. рис. 1) .
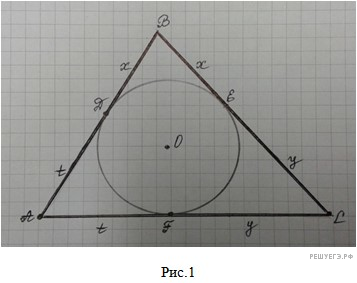
Доказательство. Пусть F, E — точки касания сторон АС и BC соответственно, Обозначим BD = BE = x, AD = AF = t, CE = CF = y. Имеем:
Мы получили: 
В соответствии с доказанным выше в основной задаче будем иметь (см. рис. 2):
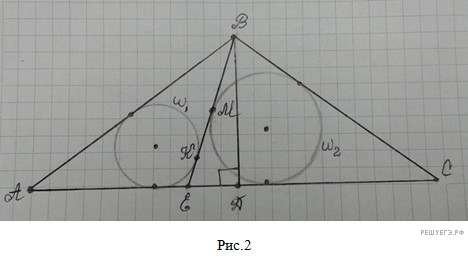
В ΔCBE 
в ΔABE 
Но
Так как AB = BC (это по условию), то: 
что и требовалось доказать.
б) AC = AE + CE = 9 + 15 = 24. Если AB = BC = x, то p(ABC) = x + 12, по формуле Герона:
это с одной стороны.
С другой же стороны, 
Значит,
Пусть D — середина АС. Тогда: BD ⊥ AC, BD = 2S(ABC) : AC = 216 : 24 = 9. DE = AD − AE = 3.
В прямоугольном ΔBDE 
Если r1 — радиус окружности ω1, то
Если r2 — радиус окружности ω2, то:
Ответ: 1.
Критерии проверки:| Критерии оценивания выполнения задания | Баллы |
|---|
| Имеется верное доказательство утверждения пункта а и обоснованно получен верный ответ в пункте б. | 3 |
| Получен обоснованный ответ в пункте б. ИЛИ Имеется верное доказательство утверждения пункта а и при обоснованном решении пункта б получен неверный ответ из-за арифметической ошибки. | 2 |
| Имеется верное доказательство утверждения пункта а. ИЛИ При обоснованном решении пункта б получен неверный ответ из-за арифметической ошибки. ИЛИ Обоснованно получен верный ответ в пункте б и использованием утверждения пункта а, при этом пункт а не выполнен. | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше. | 0 |
| Максимальный балл | 3 |
Ответ: 1.
PDF-версии: