На проекте «Вышка» каждый прыжок в воду оценивают пять судей. При этом каждый судья выставляет оценку — целое число баллов от 0 до 6 включительно. Известно, что за прыжок Тимура Ласточкина все члены жюри выставили различные оценки. По старой системе оценивания итоговый балл за прыжок определялся как среднее арифметическое всех оценок судей. По новой системе оценивания итоговый балл вычисляется следующим образом: отбрасываются наименьшая и наибольшая оценки, и считается среднее арифметическое трех оставшихся оценок.
А) Может ли разность итоговых баллов, вычисленных по старой и новой системам оценивания, быть равной 1/10?
Б) Может ли разность итоговых баллов, вычисленных по старой и новой системам оценивания, быть равной 1/15?
В) Найдите наибольшее возможное значение разности итоговых баллов, вычисленных по старой и новой системам оценивания.

 Тогда разность итоговых баллов, вычисленных по старой и новой системам оценивания равна
Тогда разность итоговых баллов, вычисленных по старой и новой системам оценивания равна 
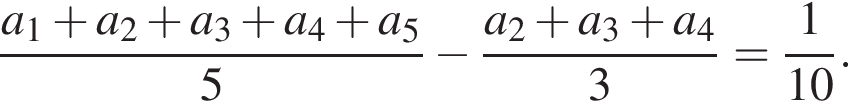


 Слева стоит четное число, а слева — нечетное. Противоречие.
Слева стоит четное число, а слева — нечетное. Противоречие.

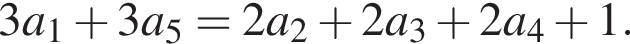 Например, годятся такие числа:
Например, годятся такие числа: 







 тогда искомая разность равна 0. Пусть
тогда искомая разность равна 0. Пусть  Если
Если  то искомая разность не больше, чем
то искомая разность не больше, чем  Ясно, что это значение достижимо, если оценки равны 0, 1, 2, 3, 6.
Ясно, что это значение достижимо, если оценки равны 0, 1, 2, 3, 6.