Боковое ребро правильной треугольной пирамиды SABC равно 10, а косинус угла ASB при вершине боковой грани равен 
Точка M — середина ребра SC.
а) Докажите, что 
б) Найдите косинус угла между прямыми BM и SA.
Решение. а) Проекция точки S на плоскость ABC — точка H, центр правильного треугольника ABC. Поэтому прямая AH содержит высоту треугольника ABC, значит,
тогда, по теореме о трех перпендикулярах, 
б) Пусть N — середина 
Поскольку 
по теореме о средней линии треугольника, угол BMN искомый. Найдём стороны треугольника 
По теореме о средней линии треугольника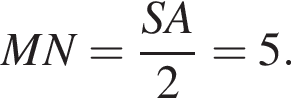 
По теореме косинусов из треугольника BSM получаем:
Чтобы найти BN, найдём сначала сторону основания по теореме косинусов из треугольника 
Теперь 
как высота в равностороннем треугольнике со стороной 
Осталось вычислить косинус нужного угла:
Ответ: 
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Имеется верное доказательство утверждения пункта a) и обоснованно получен верный ответ в пункте б) | 3 |
| Получен обоснованный ответ в пункте б) ИЛИ имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | 2 |
| Имеется верное доказательство утверждения пункта а) ИЛИ при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки, ИЛИ обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | 1 |
| Решение не соответствует ни одному из критериев, приведённых выше | 0 |
| Максимальный балл | 3 |