При каких значениях параметра a для любых значений параметра b хотя бы при одном значении параметра с система уравнений
имеет решения?
Решение. Ясно, что при 
система имеет единственное решение
которое выражается через a и c однозначно, то есть существует для любых a и 
При 
если умножить второе уравнение на b и из полученного уравнения вычесть первое уравнение системы, то будем иметь
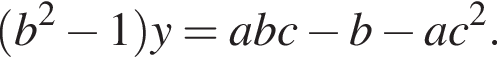
Если же умножить на b первое уравнение и из полученного уравнения вычесть второе уравнение системы, то
Таким образом, исходная система равносильна системе
При любом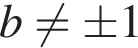 
полученная система имеет единственное решение.
Если 
то система будет иметь решения если существуют a и c удовлетворяющие уравнению 
Рассматривая его как квадратное относительно параметра с, приходим к выводу, что оно будет иметь хотя бы одно решение, если 
и 
т. е. если 
При 
приходим к рассмотрению уравнения 
Решая неравенство 
где находим, что 
Система должна иметь решения для любых значений b, поэтому найденные множества значений параметра а следует пересечь.
Ответ: 
| Критерии оценивания ответа на задание С5 | Баллы |
|---|---|
| Обоснованно получен верный ответ. | 4 |
| Рассмотрены все возможные случаи. Получен верный ответ, но решение либо содержит пробелы, либо вычислительную ошибку или описку. | 3 |
| Рассмотрены все возможные случаи. Получен ответ, но решение содержит ошибки. | 2 |
| Рассмотрены некоторые случаи. Для рассмотренных случаев получен ответ, возможно неверный из-за ошибок. | 1 |
| Все прочие случаи. | 0 |
| Максимальное количество баллов | 4 |