Тип Д10 C2 № 511273 
Сложная стереометрия. Круглые тела
i
Все плоские углы при вершине S пирамиды SABC прямые.
а) Докажите, что точка S, точка пересечения медиан треугольника ABC и точка, равноудаленная от вершин пирамиды (центр описанной сферы), лежат на одной прямой.
б) Найдите радиус сферы вписанной в пирамиду SABC, если известно, что SA = 2, SB = 3, SC = 4.
Решение.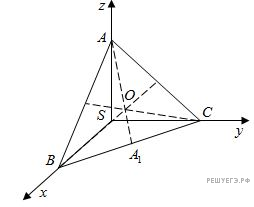 
а) Поместим пирамиду в декартову систему координат с началом S, как показано на рисунке. В качестве вершины пирамиды выберем точку А.
И пусть вершины пирамиды представляются точками: 
Точка О — место пересечения медиан грани ABC, A1 — середина отрезка BC. 
Пусть центр сферы с радиусом R, описанной около пирамиды, есть точка (m; n; p). Тогда уравнение сферы будет иметь вид: 
Поскольку точки S, A, B, C лежат на этой сфере, их коррдинаты удовлетворяют уравнению сферы. Тогда будем иметь систему
Вычитая из второго уравнения первое, получим:
Аналогично вычислим: 
Теперь найдем координаты точки О. Ясно, что:
Уравнение прямой SO будет иметь вид:
или
Если центр описанной окружности принадлежит прямой SO, то координаты точки 
обязаны удовлетворять полученноой системе. Проверим.
Получены верные равенства. Требуемое доказано.
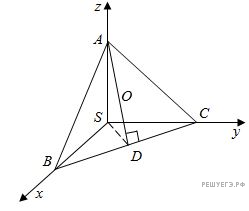
б) По услвию задачи имеем: 
Вычислим стороны треугольника ABC:
Проведем 
соедиим отрезком точки S и D. По теореме о трех перпендикулярах: 
значит,
Искомый радиус r сферы, вписанной в пирамиду, вычислим по формуле:
Ответ: б) 
Критерии проверки:| Критерии оценивания выполнения задания | Баллы |
|---|
| Обоснованно получен верный ответ. | 2 |
| Решение содержит обоснованный переход к планиметрической задаче, но получен неверный ответ или решение не закончено ИЛИ при правильном ответе решение недостаточно обосновано. | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше. | 0 |
Ответ: б)
511273
б)
PDF-версии: