В правильной треугольной пирамиде SABC с основанием ABC известны ребра 
и SC = 17. Найдите угол, образованный плоскостью основания и прямой AM, где M — точка пересечения медиан грани SBC.
Решение. Геометрический метод исследования.
Проведем: AD — медиану 
SD — апофему пирамиды 
Пусть О — центр основания пирамиды, E — проекция точки M на основание пирамиды. Соединим отрезком точки А и M, M и E.
Найдем высоту пирамиды. 
Ясно, что: 
Рассмотрим 
как два перпендикуляра к одной и той же прямой OD. Следовательно, 
Отсюда: 
по способу построения и определению угла между плоскостью и прямой — искомый угол.
Координатно-векторный метод исследования.
Поместим заданную пирамиду в декартову систему координат, как показано на рис.
Найдем координаты нужных точек: A (-4; 
0), B(-4; 
0), C(8; 0; 0), S(0; 0; 15). D (2; 
0).
Точка M делит отрезок SD в отношении 2 : 1. То есть 
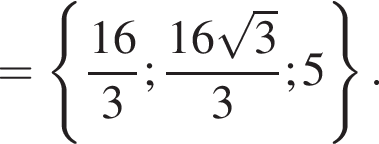
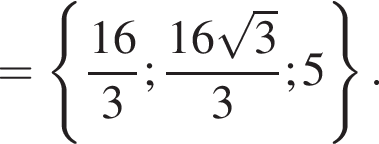
Плоскость основания пирамиды имеет уравнение z = 0, нормальный вектор которой 
Найдем синус искомого угла.
С частичным использованием векторного метода.
Так как M — точка пересечения медиан треугольника SBC, то 
Но 
следовательно, 
Найдем скалярный квадрат вектора 
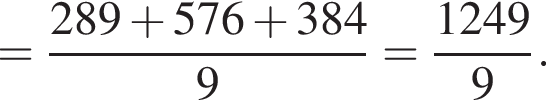
Значит, 
Выше было получено ME = 5. Отсюда: 
Ответ: 
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Обоснованно получен верный ответ. | 2 |
| Решение содержит обоснованный переход к планиметрической задаче, но получен неверный ответ или решение не закончено ИЛИ при правильном ответе решение недостаточно обосновано. | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше. | 0 |