РЕШУ ЕГЭ — математика профильная

Задания

Тип Д12 C3 № 508138 Добавить в вариант

Источник: А. Ларин: Тренировочный вариант № 93

Классификатор алгебры: Неравенства с логарифмами по переменному основанию, Неравенства смешанного типа, Неравенства, рациональные относительно логарифмической функции

Методы алгебры: Введение замены

Кодификатор ФИПИ/Решу ЕГЭ:

2.2.3 Показательные неравенства;

2.2.9 Метод интервалов.

Сложные неравенства. Неравенства различных типов

Решите неравенство $дробь: числитель: \log _2 в степени левая круглая скобка x плюс 3 правая круглая скобка 4, знаменатель: \log _2 в степени левая круглая скобка x плюс 3 правая круглая скобка левая круглая скобка минус 4x правая круглая скобка конец дроби меньше или равно дробь: числитель: 1, знаменатель: \log _2 левая круглая скобка \log _ дробь: числитель: 1, знаменатель: 2 конец дроби 2 в степени левая круглая скобка x правая круглая скобка правая круглая скобка конец дроби .$

Решение. При $x не равно минус 3$ будем иметь:

$дробь: числитель: \log _2 в степени левая круглая скобка x плюс 3 правая круглая скобка 4, знаменатель: \log _2 в степени левая круглая скобка x плюс 3 правая круглая скобка левая круглая скобка минус 4x правая круглая скобка конец дроби меньше или равно дробь: числитель: 1, знаменатель: \log _2 левая круглая скобка \log _ дробь: числитель: 1, знаменатель: 2 конец дроби 2 в степени левая круглая скобка x правая круглая скобка правая круглая скобка конец дроби равносильно$
$равносильно дробь: числитель: 1, знаменатель: \log _4 левая круглая скобка минус 4x правая круглая скобка конец дроби меньше или равно дробь: числитель: 1, знаменатель: \log _2 левая круглая скобка минус x\log _22 правая круглая скобка конец дроби$

$равносильно дробь: числитель: 2, знаменатель: \log _2 левая круглая скобка минус 4x правая круглая скобка конец дроби меньше или равно дробь: числитель: 1, знаменатель: \log _2 левая круглая скобка минус x правая круглая скобка конец дроби равносильно$
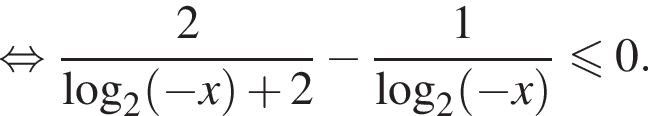
$равносильно дробь: числитель: 2, знаменатель: \log _2 левая круглая скобка минус x правая круглая скобка плюс 2 конец дроби минус дробь: числитель: 1, знаменатель: \log _2 левая круглая скобка минус x правая круглая скобка конец дроби меньше или равно 0.$

Пусть $\log _2 левая круглая скобка минус x правая круглая скобка =t.$

Тогда: $дробь: числитель: 2, знаменатель: t плюс 2 конец дроби минус дробь: числитель: 1, знаменатель: t конец дроби меньше или равно 0 равносильно дробь: числитель: 2t минус t минус 2, знаменатель: t левая круглая скобка t плюс 2 правая круглая скобка конец дроби меньше или равно 0 равносильно дробь: числитель: t минус 2, знаменатель: t левая круглая скобка t плюс 2 правая круглая скобка конец дроби меньше или равно 0.$

Решим последнее неравенство методом интервалов.

Интервалы	$левая круглая скобка минус бесконечность минус 2 правая круглая скобка$	$левая круглая скобка минус 2;0 правая круглая скобка$	$левая круглая скобка 0;2 правая круглая скобка$	$левая круглая скобка 2; плюс бесконечность правая круглая скобка$
Знак рационального выражения	−	+	−	+

Итак,

$\log _2 левая круглая скобка минус x правая круглая скобка меньше минус 2 равносильно \log _2 левая круглая скобка минус x правая круглая скобка меньше \log _2 дробь: числитель: 1, знаменатель: 4 конец дроби равносильно x больше минус дробь: числитель: 1, знаменатель: 4 конец дроби .$ $\log _2 левая круглая скобка минус x правая круглая скобка меньше минус 2 равносильно$
$равносильно \log _2 левая круглая скобка минус x правая круглая скобка меньше \log _2 дробь: числитель: 1, знаменатель: 4 конец дроби равносильно x больше минус дробь: числитель: 1, знаменатель: 4 конец дроби .$ $\log _2 левая круглая скобка минус x правая круглая скобка меньше минус 2 равносильно$
$равносильно \log _2 левая круглая скобка минус x правая круглая скобка меньше \log _2 дробь: числитель: 1, знаменатель: 4 конец дроби равносильно$
$равносильно x больше минус дробь: числитель: 1, знаменатель: 4 конец дроби .$

$0 меньше \log _2 левая круглая скобка минус x правая круглая скобка меньше или равно 2 равносильно \log _21 меньше \log _2 левая круглая скобка минус x правая круглая скобка меньше или равно \log _24 равносильно$
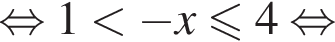
$равносильно 1 меньше минус x меньше или равно 4 равносильно минус 4 меньше или равно x меньше минус 1.$ $0 меньше \log _2 левая круглая скобка минус x правая круглая скобка меньше или равно 2 равносильно$
$равносильно \log _21 меньше \log _2 левая круглая скобка минус x правая круглая скобка меньше или равно \log _24 равносильно$
$равносильно 1 меньше минус x меньше или равно 4 равносильно минус 4 меньше или равно x меньше минус 1.$ $0 меньше \log _2 левая круглая скобка минус x правая круглая скобка меньше или равно 2 равносильно$
$равносильно \log _21 меньше \log _2 левая круглая скобка минус x правая круглая скобка меньше или равно \log _24 равносильно$
$равносильно 1 меньше минус x меньше или равно 4 равносильно$
$равносильно минус 4 меньше или равно x меньше минус 1.$

Таким образом, искомыми значениями переменной с учетом ограничения на x ,что указано выше $левая круглая скобка x не равно 3 правая круглая скобка ,$ являются элементы множества $левая квадратная скобка минус 4; минус 3 правая круглая скобка \cup левая круглая скобка минус 3; минус 1 правая круглая скобка \cup левая круглая скобка минус дробь: числитель: 1, знаменатель: 4 конец дроби ;0 правая круглая скобка .$

Ответ: $левая квадратная скобка минус 4; минус 3 правая круглая скобка \cup левая круглая скобка минус 3; минус 1 правая круглая скобка \cup левая круглая скобка минус дробь: числитель: 1, знаменатель: 4 конец дроби ;0 правая круглая скобка$

Критерии проверки:

Критерии оценивания выполнения задания	Баллы
Обоснованно получен верный ответ.	3
Обоснованно получены верные ответы в обоих неравенствах исходной системы.	2
Обоснованно получен верный ответ в одном неравенстве исходной системы. ИЛИ получен неверный ответ из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения системы неравенств.	1
Решение не соответствует ни одному из критериев, перечисленных выше.	0
Максимальный балл	3

508138

$левая квадратная скобка минус 4; минус 3 правая круглая скобка \cup левая круглая скобка минус 3; минус 1 правая круглая скобка \cup левая круглая скобка минус дробь: числитель: 1, знаменатель: 4 конец дроби ;0 правая круглая скобка$

Источник: А. Ларин: Тренировочный вариант № 93

Методы алгебры: Введение замены

Кодификатор ФИПИ/Решу ЕГЭ:

2.2.3 Показательные неравенства;

2.2.9 Метод интервалов.

Ключ

№ п/п	№ задания	Ответ
1	508138	$левая квадратная скобка минус 4; минус 3 правая круглая скобка \cup левая круглая скобка минус 3; минус 1 правая круглая скобка \cup левая круглая скобка минус дробь: числитель: 1, знаменатель: 4 конец дроби ;0 правая круглая скобка$