Найдите все значения а, при каждом из которых уравнение 
имеет ровно три различных корня.
Решение. Заданное уравнение равносильно совокупности двух уравнений:
Перепишем их так:
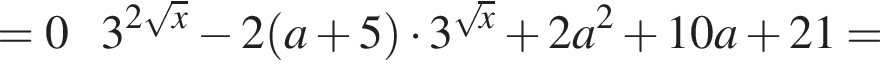
Введем новую переменную. Пусть 
Ясно, что 
следовательно, 
Имеем два алгебраических уравнения:
Для получения нужного результата рассмотрим следующие случаи:
I. Уравнение (1) имеет два подходящих различных корня, тогда как уравнение (2) будет иметь только один подходящий корень.
II. Уравнение (2) имеет два подходящих различных корня, а уравнение (1) имеет только один подходящий корень.
Случай I. Рассмотрим функцию 
Найдем ее четверть дискриминанта.
Полученный квадратный трехчлен положителен при всех значениях 
так как 
Для того чтобы уравнение (1) имело два различных корня, каждый из которых не меньше 1, необходимо и достаточно выполнение еще двух условий: 
Решим систему неравенств.
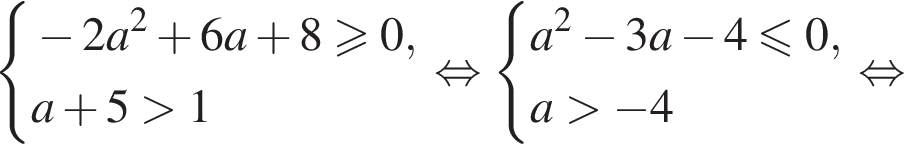
Уравнение (2) будет иметь единственный подходящий корень в двух ситуациях:
1. Четверть дискриминанта квадратного трехчлена 
окажется равной нулю.
Полученное значение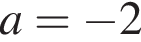 
не подходит, поскольку 
2. При положительном знаке четверти дискриминанта один из нулей функции 
окажется не меньше 1, а другой — строго меньше 1. Последнее будет иметь место, если будет выполнено условие 
Однако, 
при любом значении так как 
Таким образом, в случае I мы получаем единственное подходящее значение 
Случай II. Потребуем, чтобы уравнение (1) имело единственный подходящий корень, а уравнение (2) — два различных подходящих корня.
То, что четверть дискриминанта уравнения (1) положителен при всех значениях было показано выше. Следовательно, остается единственный вариант: число 1 на числовой прямой должно находиться между корнями квадратного трехчлена, т. е. должно выполняться неравенство 
Решим неравенство:
Чтобы уравнение (2) имело два подходящих различных корня необходимо и достаточно, чтоб было выполнено условие: 
То, что 
было показано выше. Следовательно, осталось решить систему 
Объединив результаты, полученные в двух случаях, будем иметь: 
Ответ: 
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Обоснованно получен правильный ответ. | 4 |
| С помощью верного рассуждения получено множество значений a, отличающееся от искомого конечным числом точек. | 3 |
| С помощью верного рассуждения получены все граничные точки искомого множества значений a. | 2 |
| Верно найдена хотя бы одна граничная точка искомого множества значений a ИЛИ установлено, что исходное уравнение при всех значениях a имеет единственное решение . | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше. | 0 |