Найти все значения параметра a, при которых больший корень уравнения 
на 
больше, чем квадрат разности корней уравнения 
Решение. Запишем первое уравнение так: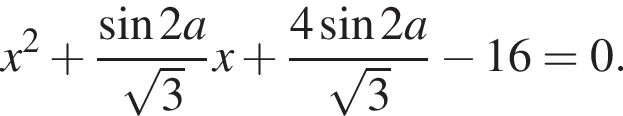 
Найдем его больший корень:
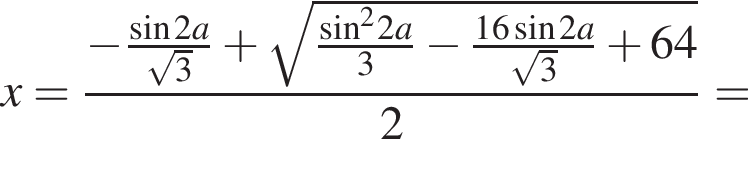
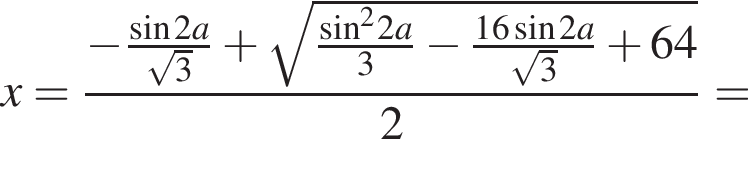
Заметим, что 
так как 
Следовательно, 
Таким образом,
Пусть второе уравнение имеет корни, равные 
и 
Выразим квадрат разности этих корней так, чтобы в дальнейшем было удобно использовать теорему Виета для приведенного квадратного уравнения:
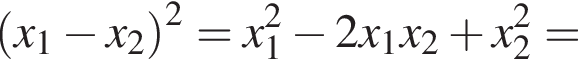
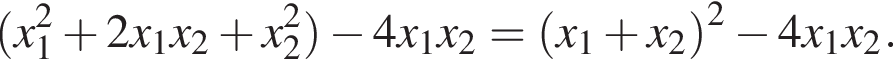
Применяя теорему Виета, получаем:
Найдем разность большего корня первого уравнения и квадрата разности корней второго уравнения : 
Эта разность по условию задачи равна 
то есть 
Решим уравнение 
относительно а:
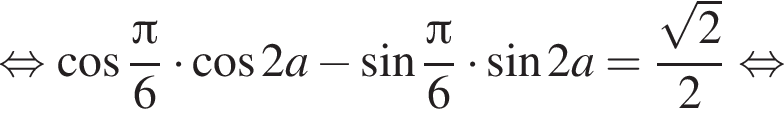
Осталось определить, при каких из найденных значений параметра уравнение 
имеет корни (теорема Виета это не гарантирует). Найдем дискриминант:
Полученное выражение не меньше 3 для любых значений а, поэтому для любых значений параметра уравнение имеет два различных корня.
Ответ: 
или 
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Обоснованно получен правильный ответ. | 4 |
| С помощью верного рассуждения получено множество значений a, отличающееся от искомого конечным числом точек. | 3 |
| С помощью верного рассуждения получены все граничные точки искомого множества значений a. | 2 |
| Верно найдена хотя бы одна граничная точка искомого множества значений a ИЛИ установлено, что исходное уравнение при всех значениях a имеет единственное решение . | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше. | 0 |
или или