
а) Решите уравнение 
б) Найдите все корни на промежутке 
Решение. а) Найдем ограничения на ![]()





Преобразуем левую часть заданного уравнения, применяя формулу тангенса суммы двух аргументов:

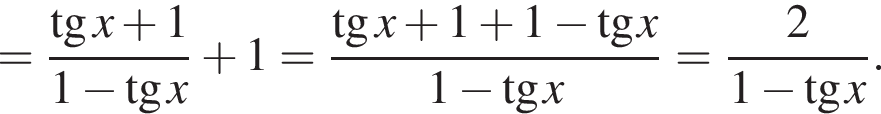







С учетом полученного результата исходное уравнение можно будет переписать так:  Теперь решим его:
Теперь решим его:


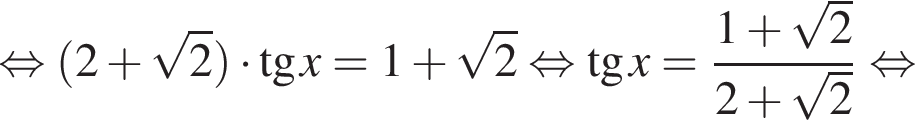







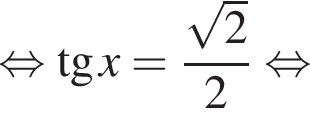

Однако, при применении в левой части исходного уравнения формулы тангенса суммы могла быть потеряна серия корней вида  Проверим. При
Проверим. При  имеем:
имеем:
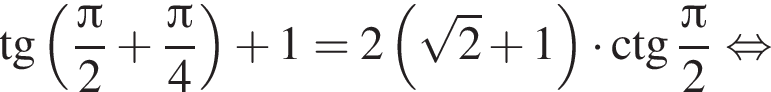
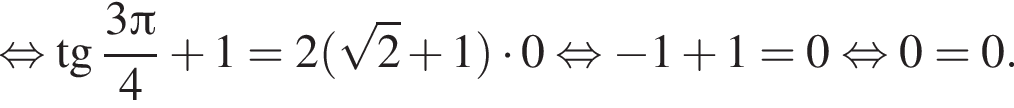
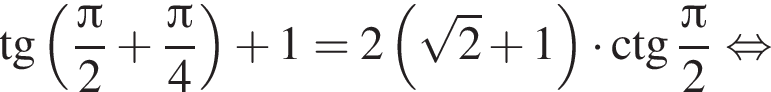


Оказалось, что числа вида  также являются корнями исходного уравнения.
также являются корнями исходного уравнения.
б) Из серии корней  получим: при
получим: при ![]()
 при
при ![]()
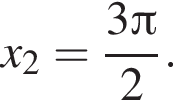
Из серии корней  поскольку
поскольку  то
то  Искомый корень из данной серии будет единственным:
Искомый корень из данной серии будет единственным: 
Замечание.
Напомним, что формула  верна только для
верна только для 
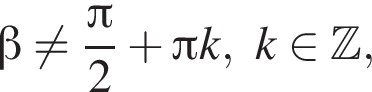
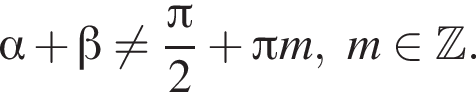 Аналогично формула
Аналогично формула  верна только для
верна только для 
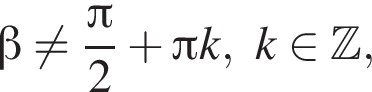

Ответ: а) 
 б)
б) 
![]()
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Обоснованно получены верные ответы в обоих пунктах. | 2 |
| Обоснованно получен верный ответ в пункте а, или в пункте б. ИЛИ получены неверные ответы из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения обоих пунктов — пункта а и пункта б. | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше. | 0 |
| Максимальный балл | 2 |

 б)
б) 

 б)
б) 