Решите систему неравенств
Решение. Рассмотрим первое неравенство. Найдем ограничения на 
Разрешенные значения x для первого неравенства: 
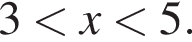Найдем значения x, при которых числитель обращается в нуль, т. е. решения уравнения 
Уравнение решим методом рационализации:
Так как 
то 4 – единственный корень рассматриваемого уравнения. При 
числитель левой части первого неравенства положительна. Теперь нам надо найти значения x, при которых знаменатель будет положительным. Решениями неравенства 
является множество 
С учетом ограничений на x решения первого неравенства системы: 
Рассмотрим второе неравенство пока что только на множестве 
Заметим, что при этих значениях x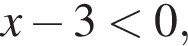 
значит,
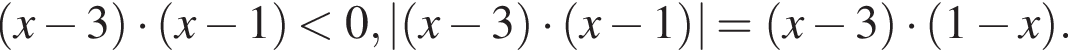
С учетом полученного результата будем иметь: 
Из-за ограниченности функции 
имеем: 
Значит,
т. е. 
для всех 
т. е. на этом множестве выражение 
принимает только положительные значения. Следовательно, дальнейшее исследование второго неравенства сводится к решению более простого неравенства: 
На рассматриваемом множестве также выполняется равенство 
значит,
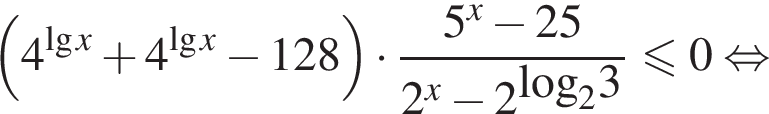
Используя единый метод рационализации, получим: 
Но для всех x, таких, что 
следовательно, 
значит, дальнейшая наша задача — рассмотрение неравенства 
на множестве
Так как 
то
На рассматриваемом множестве результат будет выглядеть так: 
Для полноты решения докажем, что число 4, которое входит в решение первого неравенства, не удовлетворяет второму неравенству.
При 
1) 
Докажем, что значение этого выражения отрицательно. Действительно,
(верное неравенство).
2) 
3) 
Произведение трех отрицательных чисел (левая часть второго неравенства) будет отрицательным. А это противоречит смыслу второго неравенства. Значит, число 4 не является решением системы.
Итак, решениями исходной системы является множество 
Замечание.
Равенство 
для 
что было использовано при решении второго неравенства, легко выводимо. Для доказательства достаточно обе части равенства прологарифмировать по 
Ответ:
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Обоснованно получен верный ответ. | 3 |
| Обоснованно получены верные ответы в обоих неравенствах исходной системы. | 2 |
| Обоснованно получен верный ответ в одном неравенстве исходной системы. ИЛИ получен неверный ответ из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения системы неравенств. | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше. | 0 |
| Максимальный балл | 3 |