Через вершину C квадрата ABCD проведена прямая, пересекающая диагональ BD в точке K, а серединный перпендикуляр к стороне AB — в точке M. Найдите 
если 
Решение. Заметим сразу, что четырехугольник AKMB — вписанный, а 
из равенства треугольников ABK и CBK по первому признаку. Обозначим за E середину 
Пусть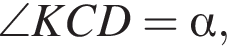 
тогда 
(из параллельности стороны и серединного перпендикуляра к другой стороне).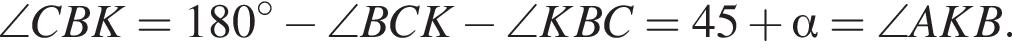 
Поскольку 
то 
тогда 
откуда треугольник CBM — равнобедренный. Значит, 
то есть 
и 
Ответ: 
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Имеется верное доказательство утверждения пункта а и обоснованно получен верный ответ в пункте б. | 3 |
| Получен обоснованный ответ в пункте б. ИЛИ Имеется верное доказательство утверждения пункта а и при обоснованном решении пункта б получен неверный ответ из-за арифметической ошибки. | 2 |
| Имеется верное доказательство утверждения пункта а. ИЛИ При обоснованном решении пункта б получен неверный ответ из-за арифметической ошибки. ИЛИ Обоснованно получен верный ответ в пункте б и использованием утверждения пункта а, при этом пункт а не выполнен. | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше. | 0 |
| Максимальный балл | 3 |